Succesive progressions how to solve mpsm kelantan
Hi Maryah, do you mean question 4?
hi i tried to send via email but unreceived. can you tell me how to send here and disclose the attchment picture of question
Question
- Diagram 1 shows the circles formed from the vortex. The resulting circle has the same center. The largest circle has a radius of 50 \mathrm{~m} and each successive circle has a radius which is half of the preceding circle.
Rajah 1 menunjukkan bulatan-bulatan yang terbentuk daripada pusaran air. Bulatan yang terhasil mempunyai pusat yang sama. Bulatan yang paling besar mempunyai jejari 50 \mathrm{~m} dan jejari setiap bulatan yang seterusnya adalah separuh daripada bulatan sebelumnya.
Diagram 1
Rajah 1(a) Find the circumference of the seventh vortex circle in terms of \pi
[3 marks] Cari lilitan bulatan pusaran air yang ke tujuh dalam sebutan \pi
[3 markah]
(b) Which circle has a circumference of \frac{25}{64} \pi \mathrm{m}
[2 marks] Bulatan yang manakah mempunyai lilitan \frac{25}{64} \pi \mathrm{m}.
[2 markah]
(c) Find the circumference if the resulting number of circles disappears from view.
Cari jumlah lilitan jika bilangan bulatan yang terhasil hilang daripada pandangan
[2 marks]
Answer
Hi maryah, for part (a), we can find the circumference by finding the radius of the seventh vortex circle first because circumference = 2\pi j (I used j here so that it wouldn’t be confused with the r in GP)
“The radius of the biggest circle is 50m, and successive circle has a radius which is half of the preceding circle”
So we know this is a GP (geometric progression), where a = 50 and r = \frac{1}{2}
To find radius of seventh circle, T_7 (7th term in the GP), we use the formula
T_n = ar^{n-1}, r in this case is \frac{1}{2}
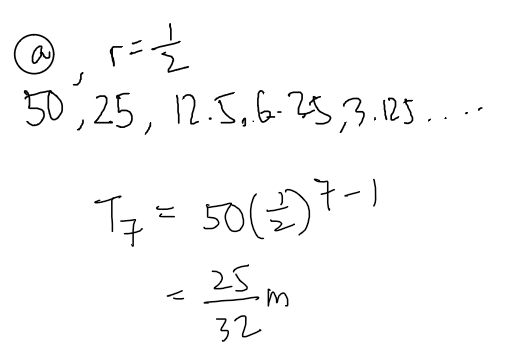
So \frac{25}{32}m is the radius of the 7th circle.
Circumference = 2 \pi r = 2 \pi (\frac{25}{32}) = \frac{25}{16} \pi m
For part (b), it is like a reverse of the steps in part (a).
We know that circumference = 2\pi j
So we equate it with the given value in the question, that is \frac{25}{64} \pi m.

Again, we use the formula T_n = ar^{n-1}. But this time we need to find n instead.
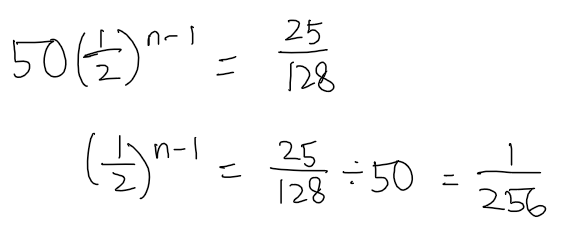
Log both sides:
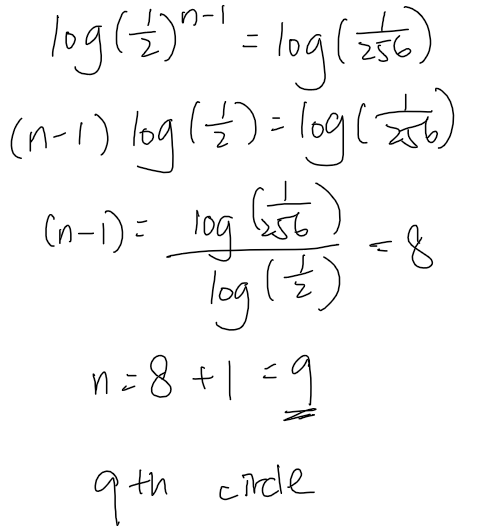
For part (c), the wording is a bit confusing.
“Find the circumference if the resulting number of circles disappears from view.”
the BM version is clearer: “Cari jumlah lilitan jika bilangan bulatan yang terhasil hilang daripada pandangan”
So they are asking for the sum of all the circumferences
What does this mean? Sum to infinity.
Since our initial GP is radius, not circumference, so we just find sum to infinity of the radii and then multiply it with 2 \pi.
So, sum of all the radii = 100 m
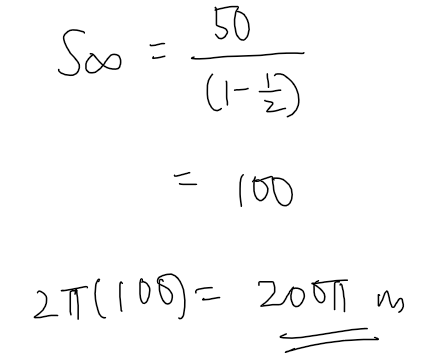
Sum of all the circumferences = 2 \pi (sum of radii) = 2 \pi (100) = 200 \pi m
Why does this work?
Sum of all the circumferences = 2 \pi j_1 + 2 \pi j_2 + 2 \pi j_3 + 2 \pi j_4 + ... 2 \pi j_n = 2 \pi (j_1 + j_2 + j_3 + j_4 + ... + j_n) = 2\pi (sum of radii)
Hope this helps! 
Hi thanks for replying about geometric progression.a) i wouldnt have calculate in terms of radius but i might have done the circumference
No worries! The question gave radius so the most direct approach would be radius, but using diameter is perfectly fine too as long as you get the same answer 

