Addmath SPM Integration

SPM
#1

855411f7810948ed58e89281f1b37c34f922228b0
855411f7810948ed58e89281f1b37c34f922228b01885×1919 247 KB

Anyone knows how to do this? Thanks

#2

Question

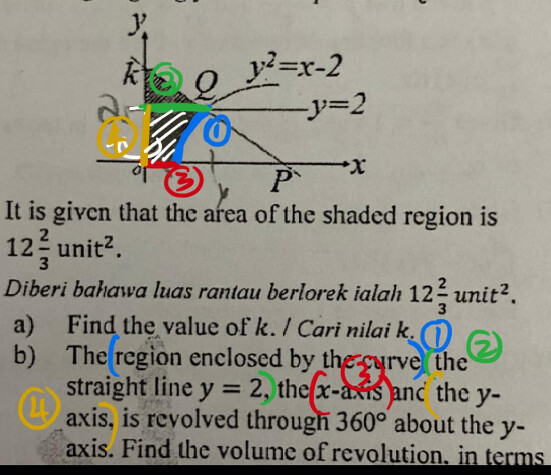
  1. Diagram below shows the straight line P Q and the straight line y=2 intersecting the curve y^{2}=x-2 at point Q. / Rajah di bawah menunjukkan garis lurus P Q dan garis lurus y=2 bersilang lengkung y^{2}=x-2 pada titik Q.
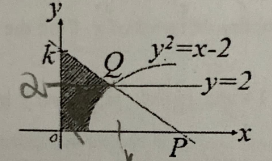
    image

It is given that the area of the shaded region is 12 \frac{2}{3} unit ^{2}.
Diberi bahawa luas rantau berlorek ialah 12 \frac{2}{3} unit { }^{2}.
a) Find the value of k. / Cari nilai k.
b) The region enclosed by the curve, the straight line y=2, the x-axis and the y axis, is revolved through 360^{\circ} about the y axis. Find the volume of revolution in terms of \pi.

Answer

Hi weiling,
For part (a), we need to split the area of shaded region into two parts:
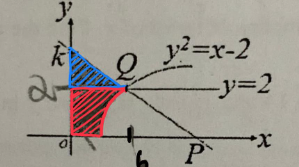
image
for the blue triangle’s area, we would use the following formula: \frac{1}{2} \times length \times height
height is (k-2), for length we just need to find the x-coordinate where the curve y^2=x-2 and line y=2 intersect.
Substituting y=2 into the equation of the curve gives:
2^2=x-2
4=x-2
x=6

And so, the area of the triangle is \frac{1}{2} \times 6 \times (k-2) = 3(k-2)

For the area shaded in red, we would need to integrate the curve with respect to y.
The general formula is \int_a^b x \space dy
Substituting a (lower bound) as 0 and b (upper bound) as 2, we get:
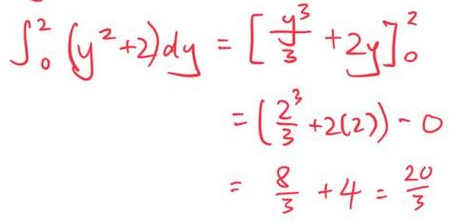
image

blue area + red area = total area
Again, we use substitution to solve for k.
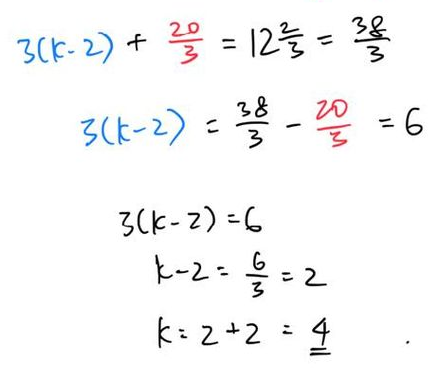
image

(b)

For part (b), the volume is not the same region as in part (a) revolved around y-axis. If you read the question carefully, it only wants the red area in part (a) revolved around y-axis.
image

The general formula for volume (revolved around y-axis) is \pi \int_a^b x^2 \space dy
Again, we substitute a (lower bound) as 0 and b (upper bound) as 2:
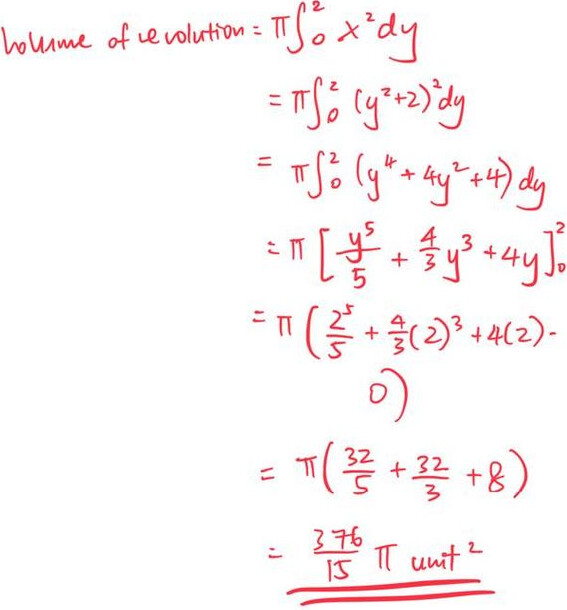
image

***edit: should be unit ^3 not unit ^2

Hope this helps! Feel free to clarify if you don’t understand anything! :slight_smile:

#3

Thank you so much for ur clear explaination

#4

Is the keyword here about the y axis (finding area revolution) but what does enclosed mean about the curve

#5

Hi maryah, apologies for the late reply, I’m not too sure what you mean but “enclosed” basically mean “surrounded”
So for b), the region is actually enclosed/surrounded on 4 sides: (with each side representing a different colour as drawn in the diagram)

  1. curve (blue)
  2. straight line y=2 (green)
  3. x-axis (red)
  4. y-axis (yellow)

I think the keyword would be finding the volume of revolution, but first you need to know which region the question is asking for and whether if it’s revolution about x/y-axis. Hope this helps :sweat_smile: