Physics Question
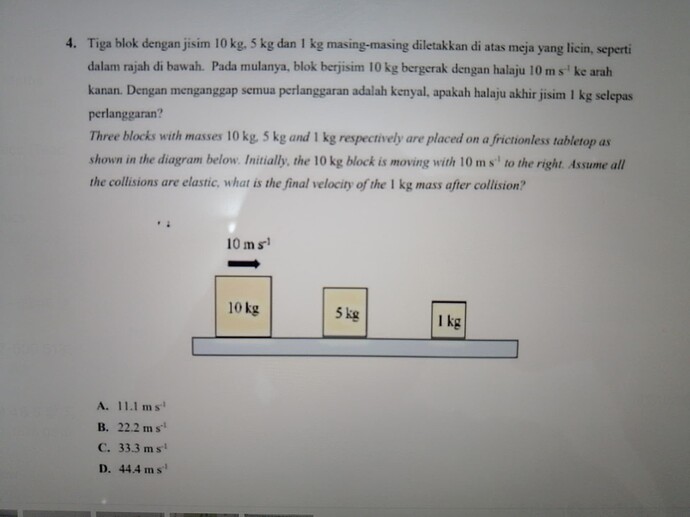
4.Tiga blok dengan jisim 10 \mathrm{~kg}, 5 \mathrm{~kg} dan 1 \mathrm{~kg}
masing-masing diletakkan di atas meja yang licin, seperti dalam rajah di bawah. Pada mulanya, blok berjisim 10 \mathrm{~kg} bergerak dengan halaju 10 \mathrm{~m} \mathrm{~s}^{-1} \mathrm{ke} arah kanan. Dengan menganggap semua perlanggaran adalah kenyal, apakah halaju akhir jisim I \mathrm{~kg} selepas perlanggaran?Three blocks with masses 10 \mathrm{~kg} 5 \mathrm{~kg} and 1 \mathrm{~kg} respectively are placed on a frictionless tabletop as shown in the diagram below. Initially, the 10 \mathrm{~kg} block is moving with 10 \mathrm{~m} \mathrm{~s}^{-1} to the right. Assume all the collisions are elastic, what is the final velocity of the 1 \mathrm{~kg} mass after collision?
A. 11.1 m s^{-1}
B. 22.2 ms^{-1}
C. 33.3 m s^{-1}
D. 44.4 ms^{-1}
Physics Solution
Notice that the question mentions “assume all collisions are elastic”, what do we know about an elastic collision?
- total momentum before and after collision are conserved
- total kinetic energy before and after collision are conserved.
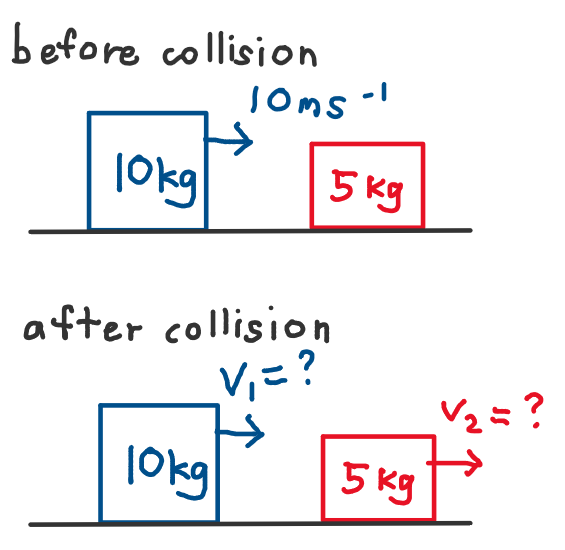
Using the formula
m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2
we get
10(10) + 5(0) = 10v_1 + 5v_2
100 = 10v_1 + 5v_2
20 = 2v_1 + v_2
v_2=20-2v_1 ------ (1)
Since we cannot use one equation to solve for 2 unknowns, we have to use the energy conservation formula.
KE before collision = KE after collision
0.5(10)(10)^2 = 0.5(10)v_1^2 + 0.5(5)v_2^2
500 = 5v_1^2 + 2.5v_2^2
200=2v_1^2 + v_2^2 ------(2)
Sub (1) into (2)
200=2v_1^2 + (20-2v_1)^2
6v_1^2 -80v_1 + 200 = 0
3v_1^2 -40v_1 + 100 = 0
(3v_1 -10) ( v_1-10) = 0
We reject v_1=10 because this would mean that the 5kg block would remain stationary and no KE is transferred to the 5kg block. It doesn’t make sense, right?
v_1= \frac{10}{3}, v_2=\frac{40}{3}
We don’t look at v_1 anymore because there would be no further collision between the 10kg and 5kg block as v_1<v_2
So the second collision would be between the 5kg block and the 1kg block.
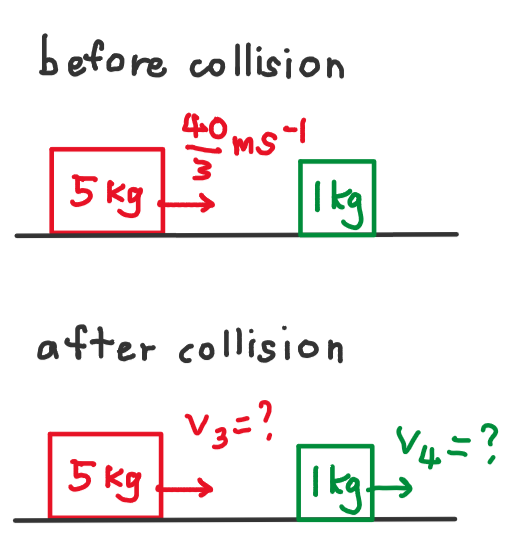
We apply the same steps we used previously to solve:
5( \frac{40}{3}) + 1(0) =5v_3 + 1v_4
200=15v_3 + 3v_4
v_3= \frac{200-3v_4}{15} ------ (3)
0.5(5)( \frac{40}{3})^2= 0.5(5)v_3^2 + 0.5(1)v_4^2
\frac{4000}{9}=\frac{5}{2}v_3^2+\frac{1}{2}v_4^2
8000=45v_3^2 + 9v_4^2 ------(4)
Substitute (3) into (4) ,
8000=45 (\frac{200-3v_4}{15})^2 + 9v_4^2
8000 = \frac{45}{225}(40000 -1200v_4 +9v_4^2) +9v_4^2
54v_4^2-1200v_4=0
v_4(54v_4-1200)=0
We reject v_4=0 because some kinetic energy must be transferred to the 1kg block.
v_4=\frac{1200}{54}=22.2ms^{-1}
So your answer is B.
This is quite a long winded question so I hope you understand the working, if you have any doubts do feel free to clarify! 
Thank you so much