I have tried to do but I’m not sure the answers.
Question
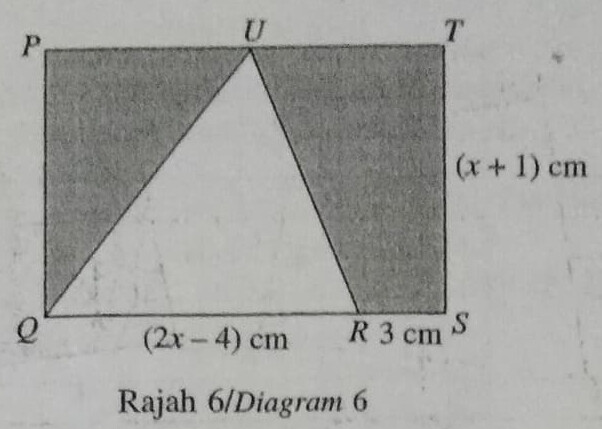
13 Rajah menunjukkan sebuah segi empat tepat PQST.
Diagram 6 shows a rectangle PQST.
(a) Buktikan bahawa luas kawasan yang berlorek, f(x) dalam rajah itu ialah f(x)=x^2 + 2x + 1.
Prove that the area of the shaded region f(x), in the diagram is f(x)=x^2 + 2x + 1.
[4 markah/4 marks](b)(i) Tandakan pintasan-x dan pintasan-y bagi graf f(x)=x^2 + 2x + 1 pada paksi yang disediakan di ruang jawapan. Seterusnya, lakar graf bagi f(x)=x^2 + 2x + 1.
Mark the x-intercept and y-intercept of the graph f(x)=x^2 + 2x + 1 on the axis provided in the answer space. Hence sketch the graph of f(x)=x^2 + 2x + 1.(ii) Diberi graf bagi f(x)=x^2 + 2x + 1 untuk x>n mewakili luas kawasan yang berlorek dalam rajah itu. Tentukan nilai n. Terangkan jawapan anda.
Given the graph of f(x)=x^2 + 2x + 1 for x>n represents the shaded region in the diagram. Determine the value of n. Explain your answer. [5 markah/5 marks]
Answer
Hi WanYee,
I believe that your answers are correct, for (b)(ii) I will use a different method as shown in the picture below. I’m not quite sure how to explain why n>2, this is the best I could think of. (Since the question said PQST is a rectangle then QS must be longer than TS, and QR cannot be 0 otherwise there would be no triangle)
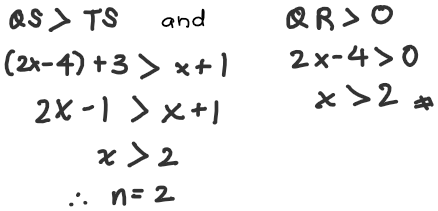
Hope this helps! 
Owww…Thank you very much Emily:grinning_face_with_smiling_eyes: