Question
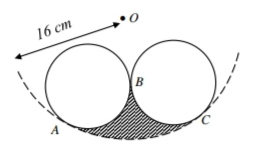
- Rajah menunjukkan dua bulatan sama dengan jejari 6 \mathrm{~cm} yang bersentuhan di B dan berada dalam satu bulatan besar berpusat \mathrm{O} dan berjejari 16 \mathrm{~cm}.
Diagram shows two identical circles with radius 6 \mathrm{~cm} touching at point B and inscribe in a large circle with centre O and a radius of 16 \mathrm{~cm}.
[Guna / Use \pi=3.142]
(a) Cari perimeter kawasan berlorek.
Find the perimeter of the shaded region.(b) Hitung luas kawasan berlorek.
Calculate the area of the shaded region.
[10 markah/marks]
Answer
Hi Farhaini,
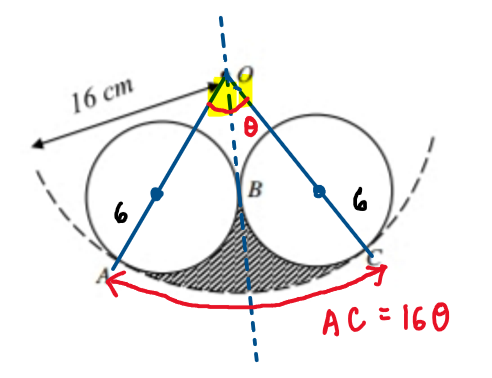
This is a slightly challenging question, for part (a), we start from arc AC as it is easier to see, you will notice that arc AC is a part of sector OAC, so we connect O to A and C to get a sector shape. (Refer to the diagram below)
Then the length of arc AC should be easy to find using the formula r\theta, but we don’t know \theta yet, so we will just leave it aside.
The line passing through O and B acts as a line of symmetry of the diagram, so everything on the LHS of the line will be the same as the RHS.
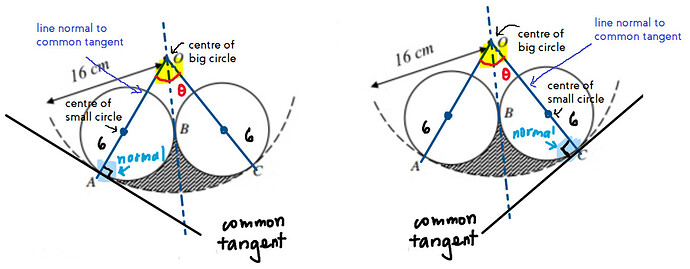
As for why line OA and OC pass through the centers of the circles: since the big and small circles intersect at A, then both circles must have a common tangent that passes through A. (Refer to the diagram below)
If line OA is normal to the common tangent, then it must pass through the centers of both big and small circles.
The same goes for the circle on the right since the diagram is symmetrical.
We apply the same concept again. Since the line passing through O and B is the common tangent to both small circles, then the line normal to line OB must pass through the centers of both small circles as well.
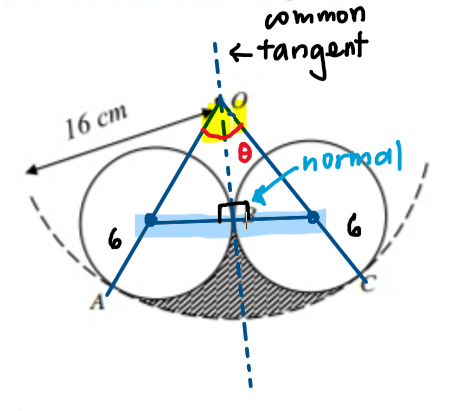
So we get an isosceles triangle at the top and two identical sectors at the bottom.
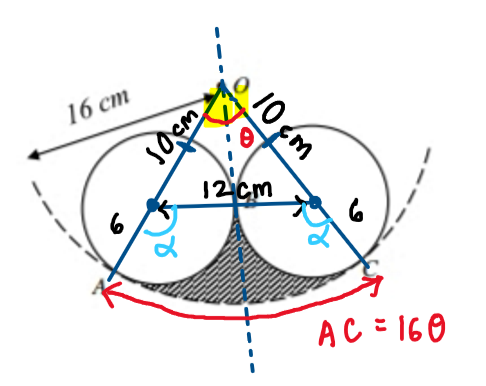
Then we continue with what we left aside in the beginning: we will use the cosine rule to find \theta, then we can find the length of arc AC.
We can find the length of arc AB using the same method as what we did for AC: find angle \alpha, then use the length of arc formula.
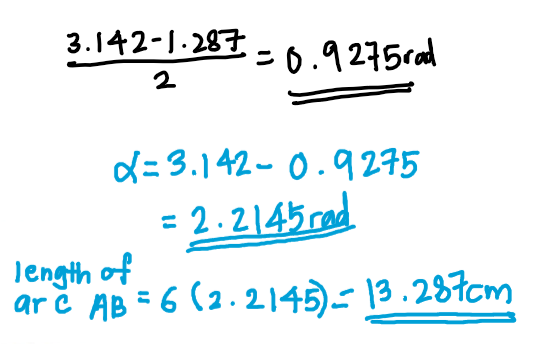
Since length of arc AB=length of arc BC, we will just multiply the length of arc AB by 2 then add it with the length of arc AC.
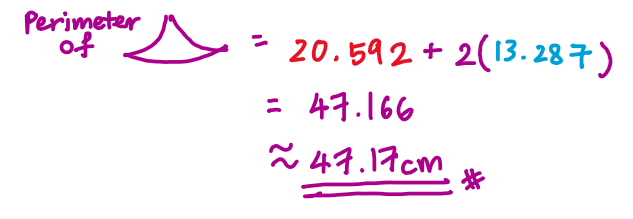
Since this post is quite long, I’ll make a separate post for part (b).
To be continued 
1 Like
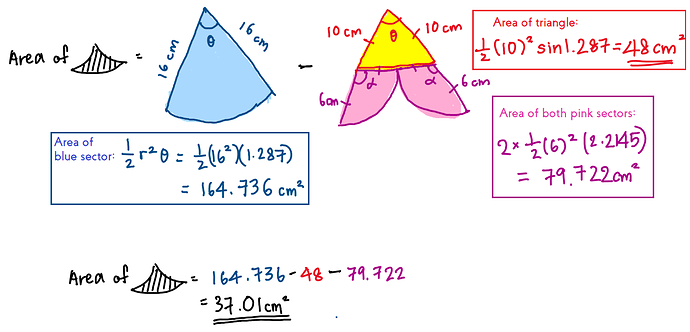
For question (b), there should be no problem if you can do part (a).
Here is my working for your reference:
Hope this helps! 
1 Like
I completely understand that 
…Thank you very much for helping me a lot although a Thank you note will not pay at all.
1 Like
You’re most welcome Farhaini, just happy to help! ^^
1 Like