Hi, may I know how to solve question 15(c)? I got the answers for (a) and (b) but couldn’t figure out how to do (c). Thank you!
Question
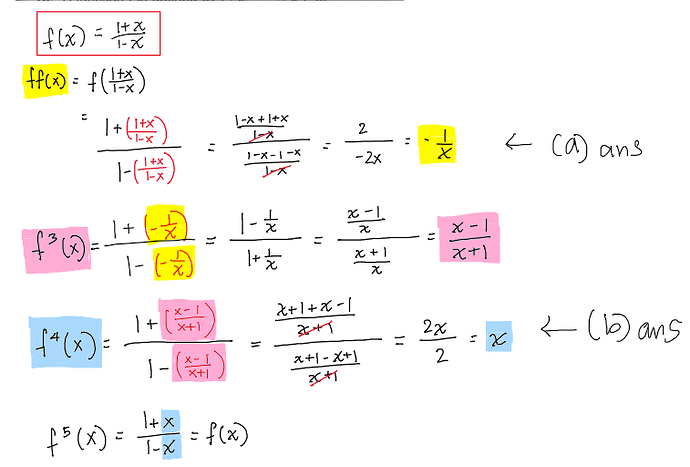
A function f is defined by f:x → \frac{1+x}{1-x}, \space x \neq 1.
Generate an expression in a similar form for
(a) f^2
(b) f^4
(c)f^{37}
Answer
Hi Jane,
The diagram below shows the working for parts (a) and (b), you already know this, but actually, we need these answers to solve part (c)!
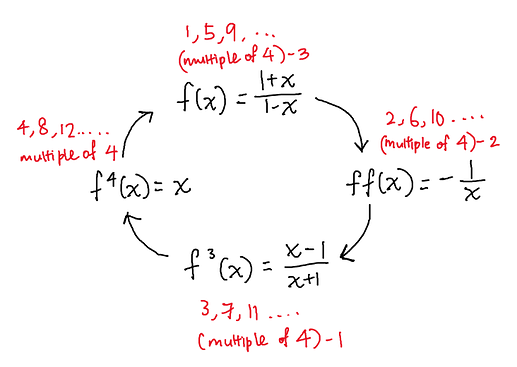
We should not do up to f^{37} one by one because it simply takes too much time. But if we do f^5(x), it’s exactly the same as f(x)!
So actually, we have a loop instead:
f^5(x)=f(x)
f^6(x)=f^2(x)
f^7(x)=f^3(x)
f^8(x)=f^4(x)
f^9(x)=f^5(x)=f(x)
f^{10}(x)=f^6(x)=f^2(x)
and so on …
From here we can see that the function repeats itself after 4 times, and the cycle repeats itself.
And getting back to our question (c): since a number being a multiple of 4 is the end of one cycle, that means f^{36}(x)=f^4(x), then f^{37}(x)=f(x), which is \frac{1+x}{1-x} as stated in the question.
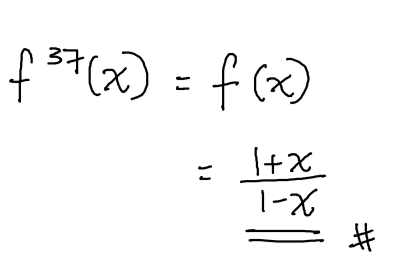
Hope this helps! 
3 Likes
Gotcha. Thank you so much for your clear explanation! Happy Chinese New Year!
1 Like
Happy Chinese New Year, Jane! (if you celebrate it 
) happy to help as well 
1 Like