Question
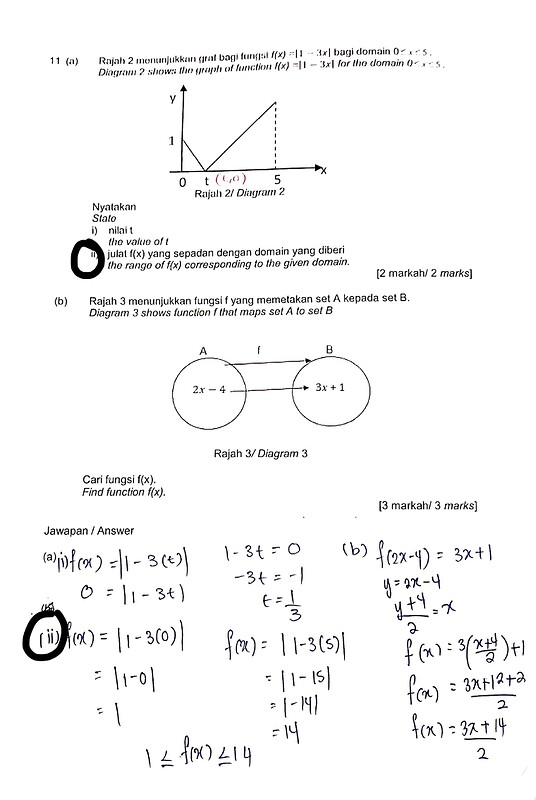
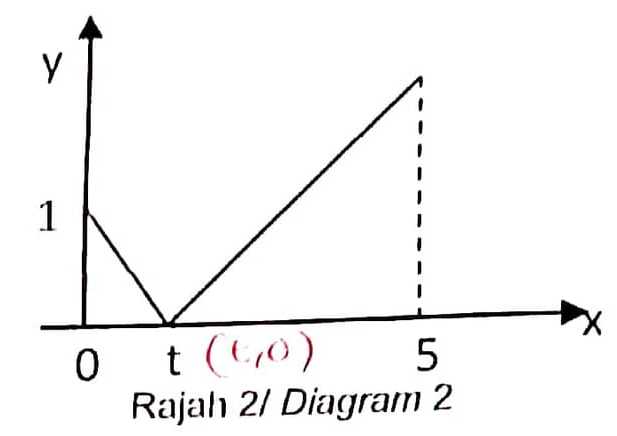
Rajah 2 menunjukkan graf bagi fungsi f(x) = |1-3x| bagi domain 0 \leq x \leq 5.
Diagram 2 shows the graph of function f(x) = |1-3x| for the domain 0 \leq x \leq 5.
Nyatakan
State
i) nilai t
the value of t
ii) julat f(x) yang sepadan dengan domain yang diberi
the range of f(x) corresponding to the given domain.
[2 markah/ 2 marks]
Answer
Hi Farhaini,
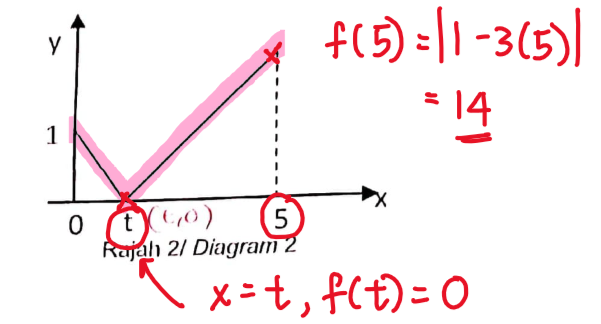
When x=0, f(0)=1. This is not the minimum value of the function, because the graph is V-shaped.
From 0 \leq x \leq t,
f(x) decreases from 1 to 0 at t,
then from t \leq x \leq 5,
f(x) increases from 0 to 14.
So the range would be 0 \leq f(x) \leq 14, where 0 is the minimum value and 14 is the maximum value. Range is always from the minimum value to the maximum value of f(x), found by using the given domain.
Hope this helps! 
Thank youuu so muchh !