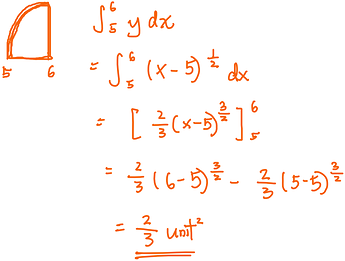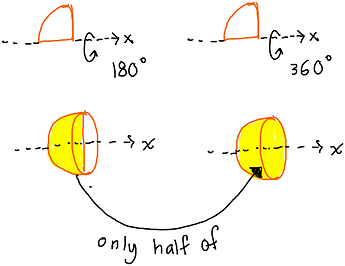Question
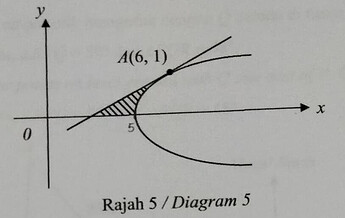
- Rajah 5 menunjukkan lengkung x=y^{2}+5 dan tangen yang menyentuh lengkung itu pada titik A(6,1).
The diagram 5 shows the curve x=y^{2}+5 and the tangent that touches the curve at point A(6,1).
Cari / Find
(a) persamaan normal pada titik A
the equation of the normal at point A
[4 markah/marks](b) luas rantau berlorek
the area of the shaded region
[3 markah/marks](c) isipadu janaan dalam sebutan \pi, apabila rantau yang dibatasi oleh lengkung dan garis lurus x=6 dikisarkan 180^{\circ} pada paksi- x
the volume of revolution, in terms of \pi, when the region bounded by the curve and the straight line x=6 is revolved about the x-axis.
[3 markah/marks]
Answer
Hi WanYee,
For part (a), before we can find the equation of the normal, we will need the gradient of the normal. But in order to find the gradient of normal, we need the gradient of tangent. We can find the gradient of tangent by expressing the x=y^2+5 equation into an equation of y in terms of x, then differentiate.
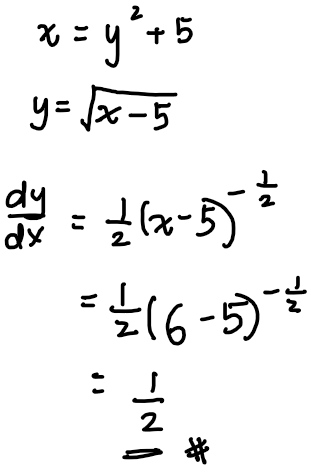
so \frac{1}{2} is our gradient of tangent, or m_1.
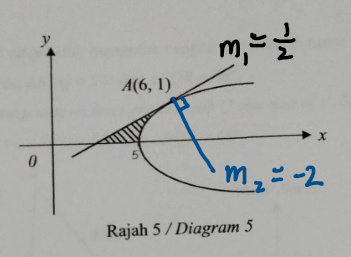
What do we know about two lines perpendicular to each other? The product of their gradients = -1. We make use of this and the equation of a straight line formula to solve (a).
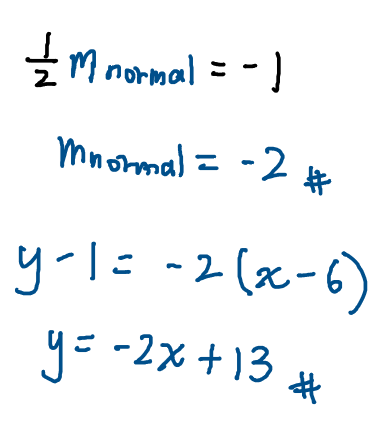
For part (b), the area of the shaded region would be a triangle minus a curved shape:
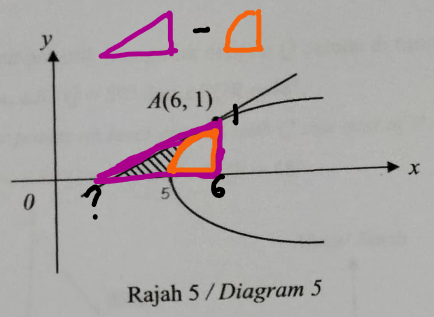
We settle the triangle first because area of a triangle is easier to solve: \frac{1}{2} \times length \times breadth
Problem: We don’t know the length.
But, the “?” in the diagram happens to be the x-intercept of the tangent passing through A. We find the equation of tangent, then substitute y=0 to find the x-intercept.
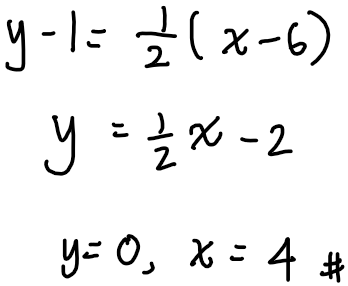

For the area of the orange shape, we integrate the curve with respect to x.
So our part (b) answer = 1unit^2 - \frac{2}{3}unit^2 = \frac{1}{3}unit^2
You might be confused, “If I integrate it from x=5 to x=6, isn’t it this shape? Why don’t I need to divide it by 2?”

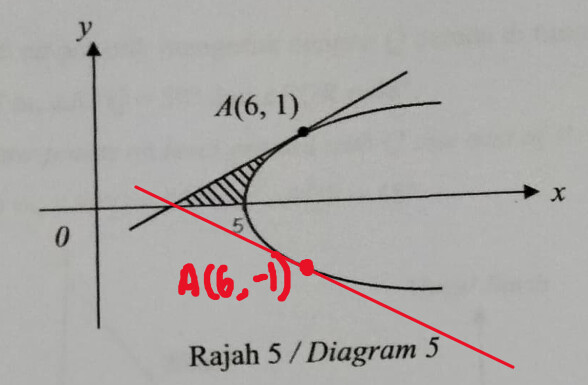
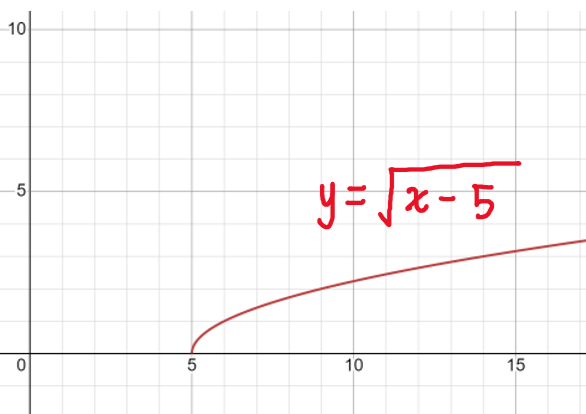
Plot twist: y=\sqrt{x-5} is NOT the same graph as x=y^2+5.
Because usually you want to get rid of the “square” you will do \pm\sqrt{},
so y=\sqrt{x-5} is only the top half of the original graph.
Extra info : If the question was A(6,-1) instead, then for part (a), we have to take the negative square root, that is y=-\sqrt{x-5}. Because the gradient of the tangent would be negative and the gradient of normal would be positive.
Finally for part (c), the 2D shape that will be rotated looks like this.
When rotated, it will look like a bowl.

As it is revolved about the x-axis, we will only use dx and not dy.
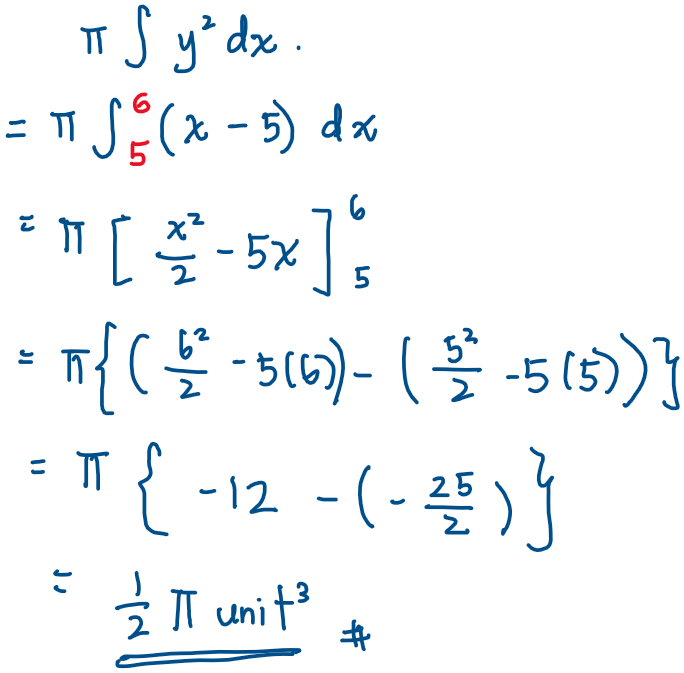
The reason we don’t need to divide the volume by 2 even though it is 180^{\circ}
and not 360^{\circ} is because the shape formed is still the same in both cases.

If the shape was like the orange shape in part (b), then we have to divide the volume by 2 if it is a 180^{\circ} rotation.
Hope this helps! 
Wow!! Thank you very much!!
Thank you very much!!