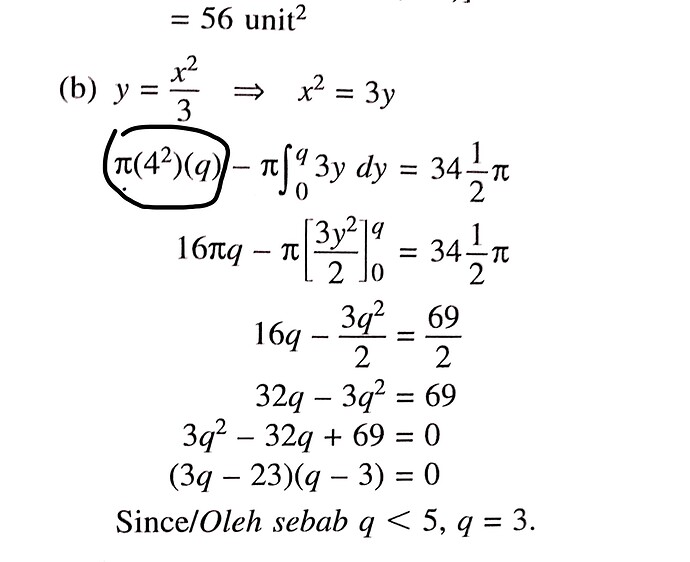Why volume of cube 4×4×q ×π ?
Addmath Integration Question
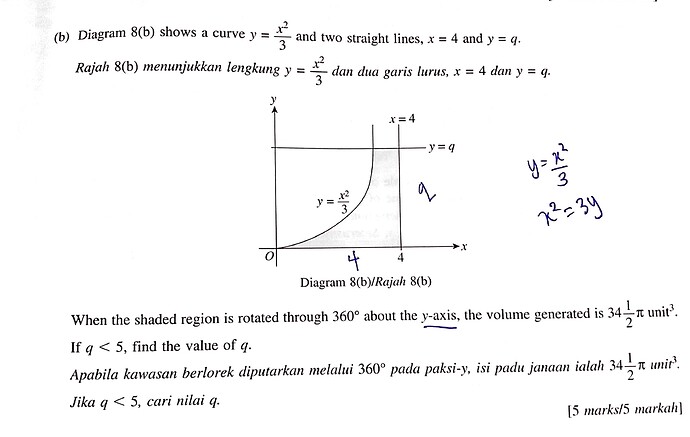
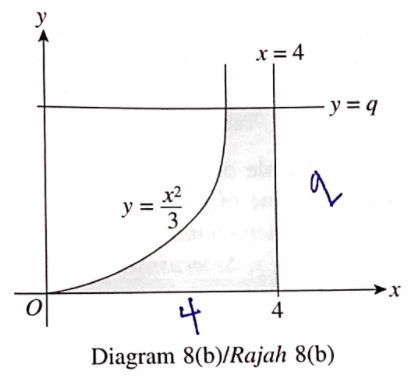
(b) Diagram 8(b) shows a curve y=\frac{x^{2}}{3} and two straight lines, x=4 and y=q.
Rajah 8(b) menunjukkan lengkung y=\frac{x^{2}}{3} dan dua garis lurus, x=4 dan y=q
y=\frac{x^{2}}{3} x^{2}=3 y
When the shaded region is rotated through 360^{\circ} about the y-axis, the volume generated is 34 \frac{1}{2} \pi unit ^{3}. If q<5, find the value of q
Apabila kawasan berlorek diputarkan melalui 360^{\circ} pada paksi-y, isi padu janaan ialah 34 \frac{1}{2} \pi unit ^{3} . Jika q<5, cari nilai q.
[5 marks/5 markah]
Addmath Integration Solution
\text { (b) } \begin{aligned}
y=\frac{x^{2}}{3} \Rightarrow x^{2}=3 y \\
\left(\pi\left(4^{2}\right)(q)\right.&-\pi \int_{0}^{q} 3 y d y=34 \frac{1}{2} \pi \\
16 \pi q-\pi\left[\frac{3 y^{2}}{2}\right]_{0}^{q} &=34 \frac{1}{2} \pi \\
16 q-\frac{3 q^{2}}{2} &=\frac{69}{2} \\
32 q-3 q^{2} &=69 \\
3 q^{2}-32 q+69 &=0 \\
(3 q-23)(q-3) &=0
\end{aligned}
Since/Oleh sebab q<5, q=3
If a straight line rotate 360 about y-axis it will become a cylinder.
1 Like
Ohh yeahh Thank you so much😊