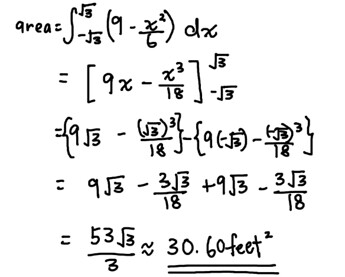Question
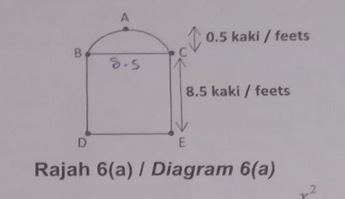
6(a) Rajah 6(a) menunjukkan pandangan hadapan sebuah pintu.
Diagram 6(a) shows the front view of a door.
BAC adalah sebahagian daripada graf y=9- \frac{x^2}{6}. A adalah titik tertinggi dari DE. Cari luas permukaan pintu.
BAC is part of the graph y=9-\frac{x^2}{6}. A is the highest point from DE. Find the surface area of the door. [3 markah / marks]
Answer
Hi Farhaini,
For this question, we cannot assume BCED is a square, because the question did not mention anything about it.
So how do we find the length of BC?
Firstly we have to plot the y=9-\frac{x^2}{6} graph.
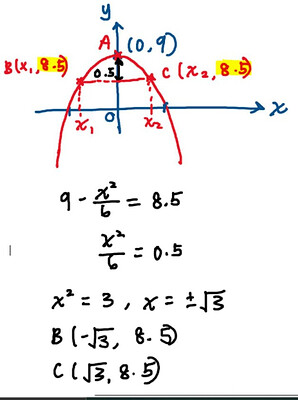
Generally, we know that when the coefficient of b is 0 in y=ax^2 + bx +c , the graph is a parabola symmetrical about the y-axis and its maximum point is the y-intercept. The question says BAC is part of the graph, and since A is the maximum point or stationary point, it is easily identified as (0,9).
The reason you cannot use A as (0,0.5) is because this pair of coordinates do not lie on the graph y=9-\frac{x^2}{6}. If you substitute x=0, you will get y=9 and not y=0.5. (LHS \neq RHS)
But this doesn’t mean the 0.5 given is useless, we can make use of it to find BC. we know that the height of A above BC is 0.5, and since BC is a straight horizontal line, we can work out that the y-coordinates of B and C:
9-0.5=8.5. To find the x-coordinates, we simply substitute y=8.5.
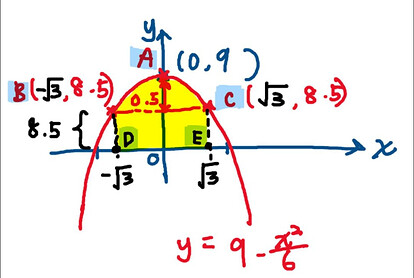
I’m not sure if you realized this, but coincidentally the whole surface area of the door is actually equal to the area under the curve integrated from -\sqrt 3 to \sqrt3 with respect to x, because:
- distance between line BC and the x-axis =8.5, which is also the same as that in diagram 6(a) where BD=CE=8.5
- height of A from x-axis=9, which is also the same as that in diagram 6(a), where the height of A from line DE=9.
And we can conclude that D and E lies on the x-axis based on these 2 reasons.
This makes the final step a lot easier as we don’t have to split the shape into two parts 
(It’s quite rare to see SPM questions with units in feets because only USA will use that kind of measurement haha 
, it’s best to give answers in units according to the question, but if the question didn’t specify, it’s usually ok to omit the unit or just write 30.60 units^2 )
Hope this helps! 
Now I understand…Thank you very much !
