Question
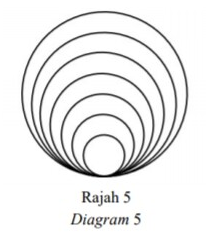
Rajah 5 menunjukkan 7 bulatan yang dibentuk dengan menggunakan seutas dawai sepanjang 140 \pi \mathrm{cm}. Jejari bagi bulatan-bulatan yang berturutan berbeza sebanyak 2 \mathrm{~cm}.
Diagram 5 shows 7 circles formed from a piece of wire with a length of 140 \pi \mathrm{cm}. The radii of the circles differ from each other successively by 2 \mathrm{~cm}.
Cari,
Find,
(a) jejari, dalam \mathrm{cm}, bagi bulatan terkecil.
the radius, in \mathrm{cm}, of the smallest circle.
[3 markah / 3 marks](b) Bilangan bulatan lengkap yang boleh dibentuk jika panjang asal dawai itu ialah 200 \pi \mathrm{cm}.
The number of complete circles can be formed if the original length of the wire is 200 \pi \mathrm{cm}.
[2 markah / 2 marks]
Answer
Hi Farhaini,
I believe that your working is correct. Yes, we do get 8.61, but we don’t round up to 9, instead we round down to 8. Because 8.61 means we can only form 8 complete circles and the 0.61 means that it is the additional incomplete circle.
You can always substitute your answers into the formula to double check:
When n=8, S_n=\frac{8}{2}(16\pi + (8-1)\times4\pi)=176\pi
When n=9, S_n=\frac{9}{2}(16\pi + (9-1)\times4\pi)=216\pi
176 \pi is less than 200\pi, which means we still have some wire left after forming 8 circles.
216\pi is more than 200\pi, which means we don’t have enough wire to form the 9th circle.
Hope this helps! 
Ohhh I see Thank you very much