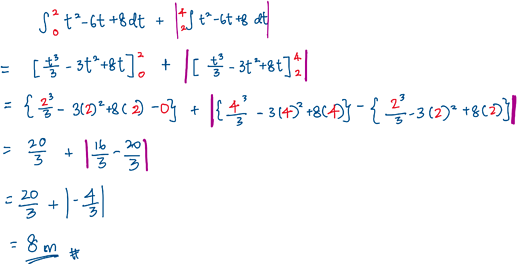Hi, how to solve this question?
*especially b
Question
12 Suatu zarah bergerak di sepanjang suatu garis lurus dan melalui satu titik tetap O. Pecutannya, a \mathrm{~m} \mathrm{~s}^{-2}, diberi oleh a=2 t-6, dengan keadaan t ialah masa, dalam saat, selepas melalui O. Halaju awal zarah tersebut ialah 8 \mathrm{~m} \mathrm{~s}^{-1}. Cari
[Anggapkan gerakan ke arah kanan sebagai positif]A particle moves along a straight line and passes through a fixed point O. It’s acceleration, a \mathrm{~m} \mathrm{~s}^{-2}, is given by a=2 t-6, where t is the time, in seconds, after passing through O. The initial velocity of the particle is 8 \mathrm{~m} \mathrm{~s}^{-1}. Find
[Assume motion to the right is positive](a) halaju minimum zarah, dalam \mathrm{m} \mathrm{s}^{-1},
the minimum velocity of the particle, in \mathrm{m} \mathrm{s}^{-1},
[4 markah/ 4 marks](b) nilai k apabila zarah sentiasa bergerak ke arah kanan selepas k saat, the value k if the particle always moves to the right after k seconds,
[2 markah/2 marks](c) jumlah jarak, dalam \mathrm{m}, yang dilalui oleh zarah dalam 4 saat pertama
the total distance, in \mathrm{m}, travelled by the particle in the first 4 seconds.
[4 markah/4 marks]
Answer
Hi Alia,
For part (a), the keyword is minimum velocity. What are the facts when a velocity is minimum or maximum? That is: \frac{dv}{dt} = 0. And a=\frac{dv}{dt}, so a=0 when velocity is minimum. We use this to find the time.
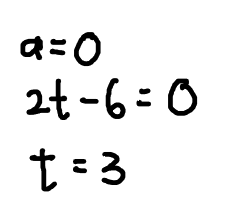
When t = 3,
- the acceleration is zero, and
- the velocity is minimum.
We then find an expression for the velocity in terms of t by integration:
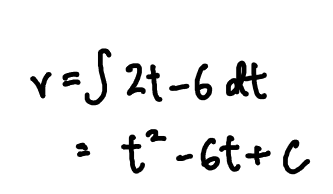
Since this is an indefinite integral (where we don’t substitute the limits), we must put +c.
We don’t know c, but we are given the initial velocity, 8ms^{-1}.
So we can conclude that when t=0, v=c.
And simply substitute all the unknowns we have found to find v_{min}.
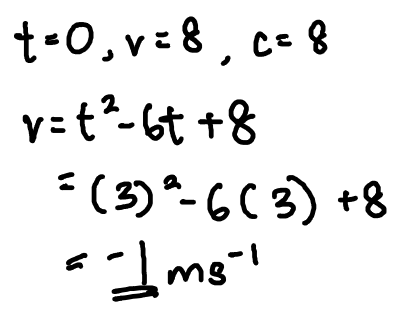
For your info, the velocity graph looks like this:
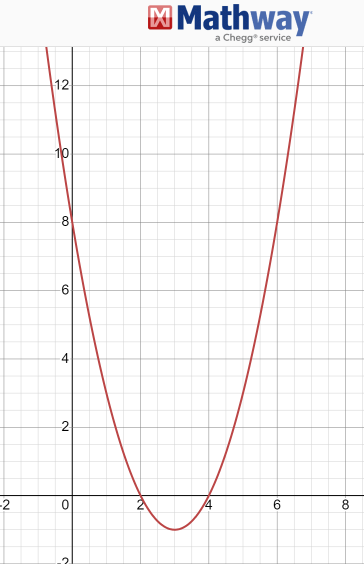
So for part (b), they want you to find t=k where the particle moves to the right after this time. And if you notice the sentence above (a), [Assume motion to the right is positive], This means that the condition v>0 must be fulfilled after t=k.
By looking at the graph earlier you can probably tell that the answer is k=4.
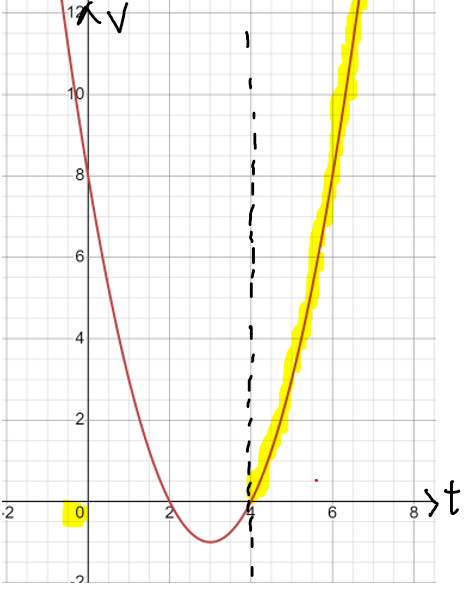
If we have to write it out, the solution looks like this:
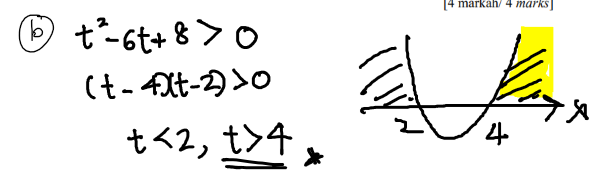
So k=4.
Since they want after and not before, we reject k=2.
Extra: If the question says “Find the ranges of values of t for which the particle moves to the right”
Then the answer would be 0<t<2 and t>4.
(c) The question wants total distance. Not displacement. Thus we cannot directly integrate from t=0 to t=4.

We cannot do this, because, from the graph shown, at t=2 to t=4, The area under the graph is negative! A negative area means the distance travelled is in the opposite direction, that is the particle moves to the left from t=2 to t=4 since we are taking motion to the right as positive.
So what we are doing when we directly integrate from 0 to 4 is that we are subtracting the two areas, not adding them up. (If you need further clarification feel free to ask ^^)
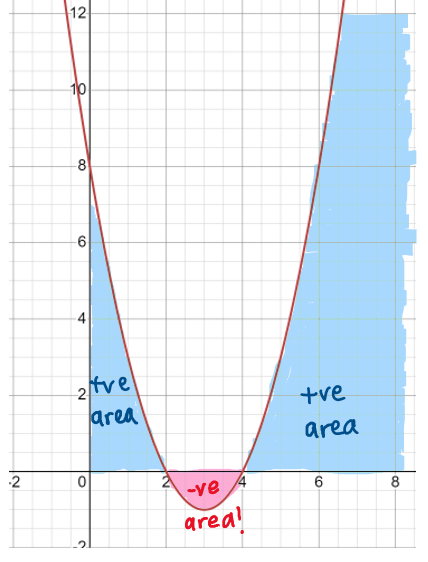
This would be the correct way to do it: split the range into two ranges, 0 to 2 then 2 to 4. Because the second area is negative, we add a modulus to it.
This means that:
From t=0 to t=2, particle has travelled \frac{20}{3}m to the right, then
from t=2 to t=4, particle travelled another \frac{4}{3}m to the left.
So that is why the modulus is there.
Hopefully this gives you a clearer idea of the question!