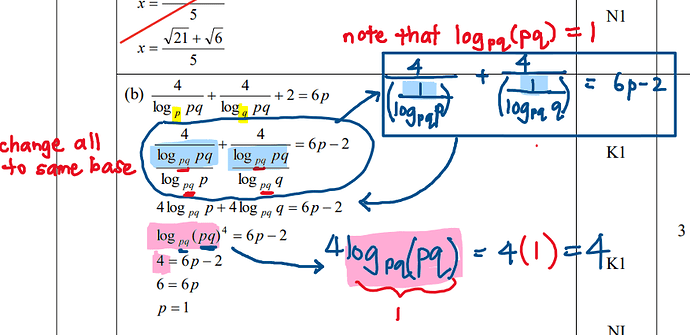
Answer
Hi Farhaini,
For this question I used a different method than the mark scheme, so I will first explain what the mark scheme did, then I will show you my method 
Mark scheme method:
What they did was basically change all the logarithms to the same base: base pq, and they simplified from there. You know that log_{10}\space 10=1 , so same goes to log_{pq}\space (pq)=1. A logarithm of a value with a base of the same value is always equal to 1.
For log_{pq}\space (pq)^4, personally I prefer to write it as 4log_{pq}\space (pq) so you can see clearly that it is equal to 4, as shown in my digital writing, but it is a matter of preference
My solution-messy and might be hard to understand, feel free to skip reading
My working is more complicated but I managed to get the same answer, don’t worry about it too much if it confuses you, just stick to the method you’re comfortable with, but it’s always good to look at other methods so that you will always have more ideas when it comes to solving problems 
For me, when I first looked at the problem I didn’t think of changing it to base pq straight away (because I didn’t really like the base to have two unknowns). So what I did was I split the pq using the multiplication of logarithms law.
From here,I then decided to change all logarithms to the same base. Doesn’t matter if it is base q or p as long as they all have the same base)
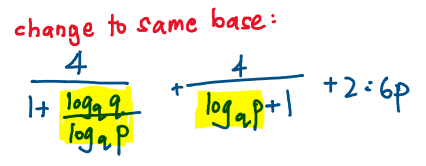
You can see I ended up with something quite complicated: a fraction inside a fraction.
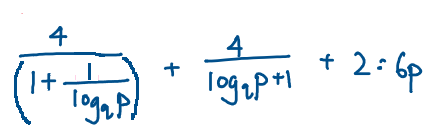
Here is the tricky magic part, you can see if I multiply the denominator of the first fraction with log_{q}\space p, I end up getting the same denominator as the second fraction!
Coincidentally, I can factorize the numerator, the top part and bottom part cancels off, I end up getting the same answer.
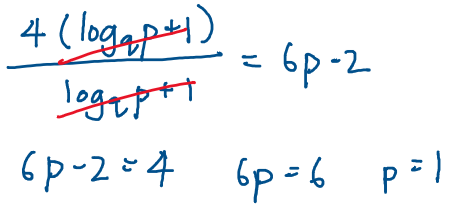
Sorry if I confused you haha, my solution is mostly trial and error and making smart guesses (maybe because I always like to complicate things haha) 
which is why I decided to explain the mark scheme method first, which is simpler and shorter No matter what method you use, as long as it is logical and within the syllabus, you should be fine!
Hope this helps! Feel free to clarify any parts which I didn’t explain well enough 
I understood both solutions. Thank you very much for helping me a lot.
I appreciate that very much ! 