Question
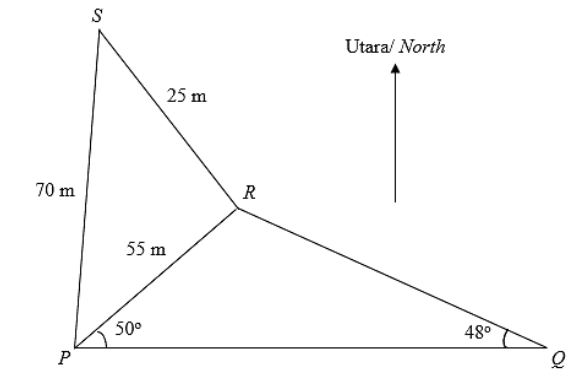
- P, Q, R dan S adalah empat titik mengufuk dengan Q berada di timur P. Diberi PR = 55 m, RS = 25 m, PS = 70 m, ∠RPQ = 50^{\circ} dan ∠PQR = 48^{\circ}.
P, Q, R and S are four points on level ground with Q due east of P. Given PR = 55 m, RS = 25 m, PS = 70 m, ∠RPQ = 50^{\circ} and ∠PQR = 48^{\circ}.
(a) Hitung
Calculate
(i) panjang PQ
the length of PQ
(ii) ∠RPS
(iii) luas segitiga PQR
the area of triangle PQR. [7 markah/marks](b) Seorang lelaki berjalan di sepanjang PQ bermula di P sehingga sampai ke X yang sama jarak dari P dan R. Hitung jarak PX.
A man walks along PQ from P until he reaches a point X which is equidistant from P and R. Calculate the distance of PX. [3 markah/marks]
Answer
Hi Farhaini,
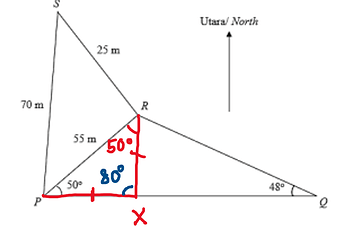
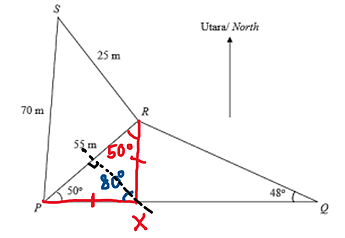
I believe the triangle should look like this:
Point X is equidistant from P and R means PX = XR. We get an isosceles triangle whose axis of symmetry is perpendicular to PR and passes through point X.
For the sketch you’ve made, it would be the case at which point R is equidistant from P and X, so PR = RX. Your triangle will still be an isosceles triangle but the axis of symmetry doesn’t pass through X, but R instead. However, this is not the question wants, even though the wording looks similar.
So the answer looks like this:
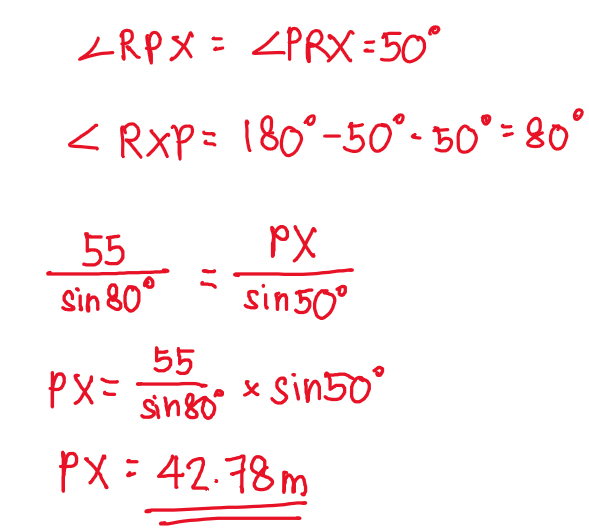
Hope this helps! 
Very clear Thank you very muchh !