Question
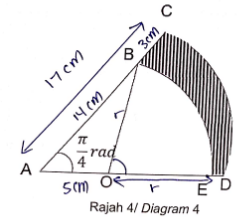
14. Rajah 4 menunjukkan sektor A C D yang berpusat A dan berjejari 17 \mathrm{~cm} . O B E ialah suatu sektor lain berpusat di O dan berjejari r.
Diagram 4 shows sector A C D with centre A and a radius of 17 \mathrm{~cm} . OBE is another sector with centre O and radius r.
Diberi bahawa B C=3 \mathrm{~cm}, O A=5 \mathrm{~cm} dan O A B=\frac{\pi}{4} radian. Hitung
It is given that B C=3 \mathrm{~cm}, O A=5 \mathrm{~cm} and O A B=\frac{\pi}{4} radians. Calculate
[Guna / Use =3.142]
(a) nilai r dalam \mathrm{cm},
value of r in \mathrm{cm},
[2 markah / 2 marks](b) B O D dalam radian,
B O D in radians,
[2 markah / 2 marks](c) luas, dalam \mathrm{cm}^{2}, rantau berlorek.
the area, in \mathrm{cm}^{2}, of the shaded region.
[4 markah / 4 marks]
Answer
Hi Farhaini,
We know that this question definitely has something to do with the circular measure chapter, but if you look closely, it is also combined with the solution of triangles chapter.
For part (a) we must look at the triangle. We know two of the lengths of the triangle and one of the angles, and the angle given is in between the two given lengths. So we know that we have to use the cosine rule in this case to find r.
For (b) , we know that in order to find \angle BOD, the easiest way would be to find \angle BOA first, then we just have to subtract \angle BOA from \pi. How do we find \angle BOA? After solving part (a), we already know all 3 lengths of the triangle, and one given angle. So we would use sine rule in this case.
(Note: I recommend “storing” the answer from part (a) into the calculator and not use a rounded value for r to be more accurate, which is why I wrote r instead of 11.05.)
If you’re using fx-570 MS like me:
You can store values using [SHIFT] [RCL] and then press a button with any pink-coloured letter from A to F, X, Y or M on the top right corner of it. And when you want to use back the stored value, just press [ALPHA] and the button that you chose.
If you’re using other calculator models then you can refer to the calculator book that comes with it 
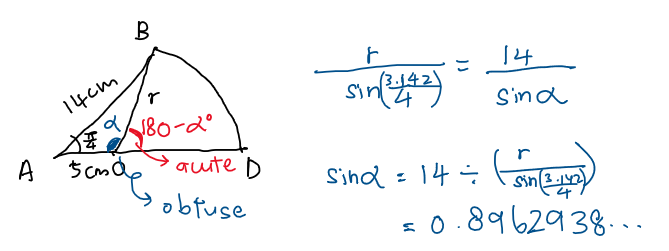
Since 1.1113 rad is smaller than \frac{\pi}{2}, it would be an acute angle which is not the case for \angle BOA because \angle BOA is obtuse.
\angle BOA= \pi - basic angle

(You can also “store” the angle into the calculator as a different letter)
And lastly for part (c), it is fairly straightforward:
Hope this helps! 
Ouhhh I seee Thank you very much!