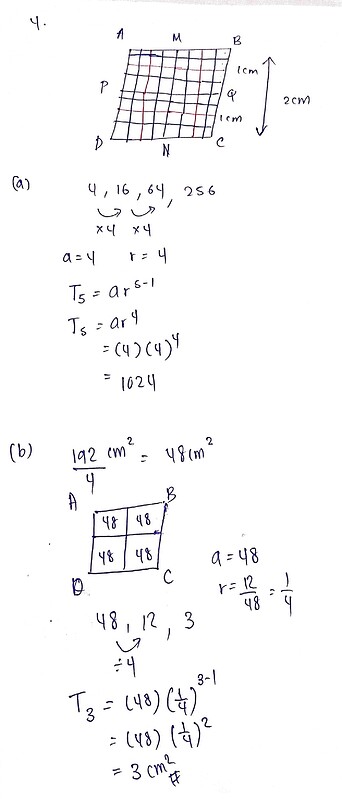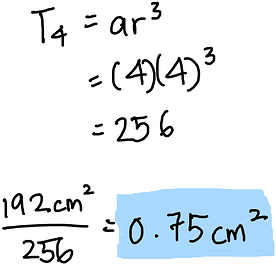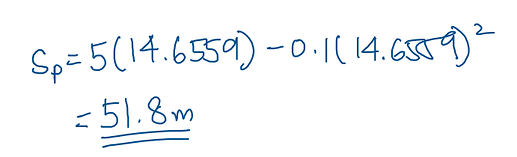Question
The diagram shows a rhombus A B C D with sides of 2 y \mathrm{~cm} each. P, Q, M and N are the midpoints of A D, B C, A B and C D respectively. P Q and M N divide A B C D into 4 similar rhombuses. Each of these four rhombuses is again divided into four parts as in the earlier process and this goes on indefinitely. Find
(a) the number of equal size rhombuses obtained after the process has been repeated five times.
(b) the area of each rhombus after the process has been repeated three times if the area of A B C D is 192 \mathrm{~cm}^{2}.The diagram shows a tube of length 155.4 \mathrm{~m} . P and Q are two balls at either end of the tube and are projected towards each other with initial speeds of 5 \mathrm{~m} \mathrm{~s}^{-1} and 10 \mathrm{~m} \mathrm{~s}^{-1} respectively. Ball P slows down at a rate of 0.2 \mathrm{~m} \mathrm{~s}^{-2} while ball Q slows down at a rate of 0.4 \mathrm{~m} \mathrm{~s}^{-2}.
Find
(a) the time taken for them to meet.
(b) the distance from the side of P to where they meet.
(c) the difference in total distance travelled between them.
Answer
Hi YiHang,
This is a rather tricky question, the reason my answer differs from Farhaini is because of the word ârepeatâ .
(a) Firstly, the question divides 1 rhombus into 4,
then they tell you to ârepeat the process five timesâ.
So from my perspective,
if I divide 4 rhombi into 16, Iâm repeating one time.
If I divide 16 rhombi into 64, Iâm repeating two times.
64 to 256: three times, and so on.
If I take 4 as T_1, then I should be looking for T_6. This can be done using the formula for GP terms: T_n = ar^{n-1}.
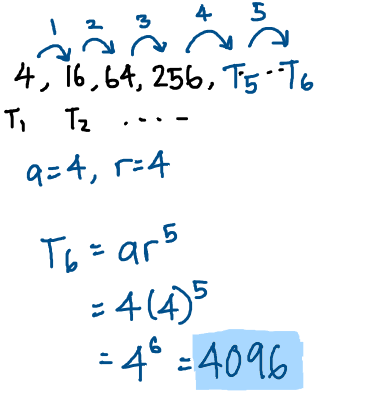
The same goes for (b), I should be looking for T_4 if I repeat the process three times:
The reason I use 4 instead of \frac{1}{4} is because I want to find the number of rhombi, then divide the total area by the number of rhombi to find each area, since the total area doesnât change.
You can also use Farhainiâs way, where she divides the area without finding the number of rhombi:
Could you share the answers of the book with us? Just to double-check. Much thanks! 
[Question 5 to be continued in next comment]
As for question 5, I donât think it has to do with progression, most probably it is from the motion of a straight line or kinematics chapter (forgot the name 
)
There are two ways to solve this: Physics approach (no integration needed) and the integration approach.
But first, let us summarize the question information:
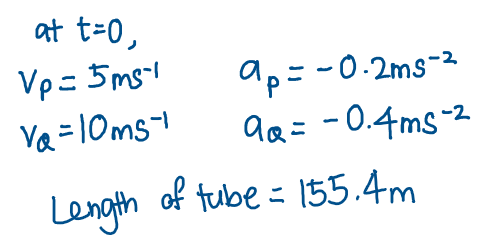
Physics approach
When P and Q meet, then we can deduce that
distance travelled by P + distance travelled by Q = length of tube
Since both balls have constant deceleration, we can use suvat for this question.
s = ut + \frac{1}{2}at^2
For this very case, I wonât be applying âmotion to the left = negative velocityâ and âmotion to the right = positive velocityâ that kind of rule. (Well, actually you can do that, then one of your decelerations will have a positive sign and you have to use modulus later on when it comes to adding the displacements)
I will only use the negative sign for deceleration because its direction opposes the motion of the ball.
Like this:
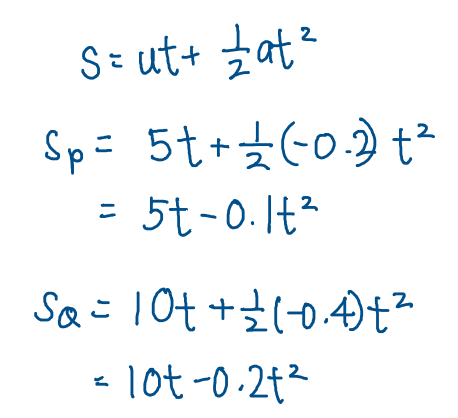
Then s_p + s_q = 155.4 from what we deduced earlier. Solving the quadratic equation gives you two values.
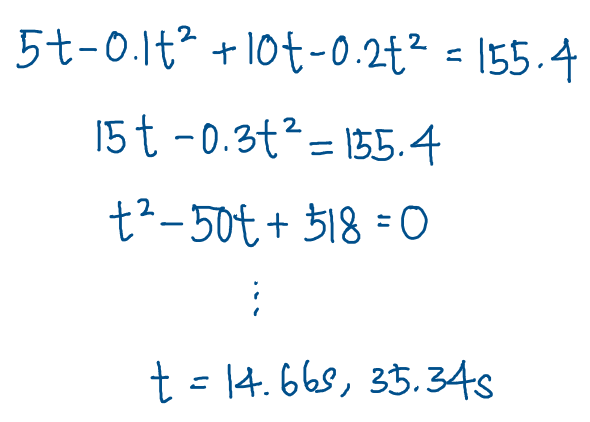
But which value to use? We take the smaller one. Use t=14.66s, and reject t=35.34s
This is because 14.66s is the first time they meet. You donât really know what does t=35.34s mean. Maybe itâs the time that they reach back their original position after they collide? But you donât know what happens after they meet. Elastic collision? Inelastic collision? Donât have to know, donât have to worry.
Part (b) and (c) becomes easy once you have solved part (a), itâs simply just substitution.
Part (b)
Part (c)
Integration method
I think this is the more appropriate way since itâs add maths after all 
, but I still wanted to show two perspectives to hopefully let you understand better. (Sorry if it confuses more)
We know that a = \frac{dv}{dt}, so integrating a will give us v.
v = \frac{ds}{dt}, so integrating v will give us s.
So we integrate twice for each ball to get two expressions for s.
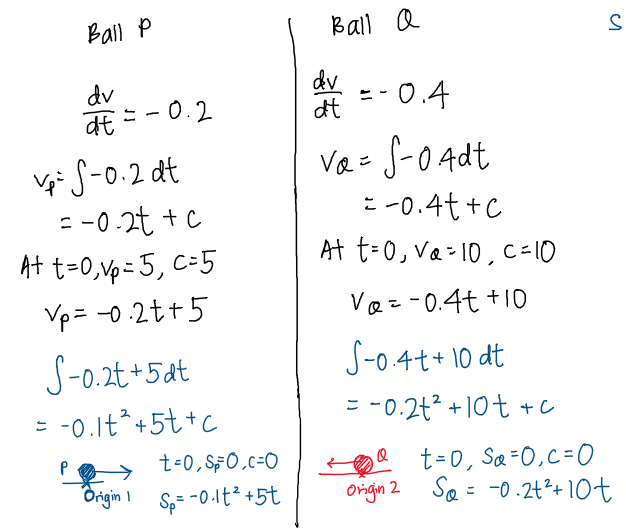
Then I use c = 0 for each ball because I have two origins. Initially both balls are at their respective origins so the displacement at t = 0 is 0 for each ball. (If youâre only using one origin for both balls, c will be different)
I get the same expression as the physics method, and the next steps are all the same.
Hope this helps, if itâs too complicated feel free to ask for further clarification, or I could think of another method to explain it to you 