Question
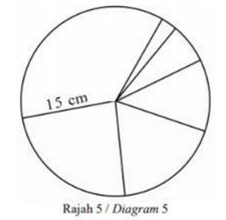
5 Satu bulatan dengan jejari 15 cm dibahagikan kepada 6 sektor, seperti dalam Rajah 5, dengan keadaan luas sektor-sektor membentuk janjang geometri.
A circle with a radius of 15 cm is divided into 6 sectors, as shown in Diagram 5, such that the angles of the sectors form a geometric progression.
Diberi bahawa luas bagi sektor yang terbesar ialah 32 kali luas sektor yang terkecil. Cari luas, dalam sebutan \pi, bagi sektor yang terbesar.
Given that the area of the largest sector is 32 times the area of the smallest sector. Find the area, in terms of \pi, of the largest sector. [6 markah / marks]
Answer
Hi Farhaini,
For the smallest angle, I’ll let it be a. Since the question said the angles form a GP, then it must mean the second smallest angle must be ar, (where r is the common ratio) the third smallest angle must be ar^2… and so on.
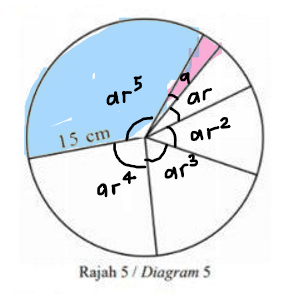
And we know that there are six sectors, and the six sectors make up a complete circle. This would mean that the sum of all six angles would be 2\pi \space rad.
Using the sum of GP formula, S_n=\frac{a(r^n-1)}{r-1},
we now have our first equation, which we will leave it aside for now.
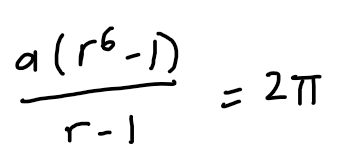
For this question, we are certain that r is larger than 1. That is only if you treat the smallest angle as the first term of the GP because the angle keeps getting bigger. If you treat the largest angle as the first term of the GP: a, then your r will be less than 1 and you should use the 1-r formula.
(But like I said, it’s not wrong to use either formula. Just that for SPM they are more specific on this so it’s best to just follow haha)
Then we need a second equation to find both a and r.
We can get this equation by using the information given by the question: Area of the sectors. Here, I used the capital letter R instead of r for radius (Not to be confused with the r in GP)

After getting r, the last few steps are fairly simple: find a, then substitute a and r to find the area of the largest sector.
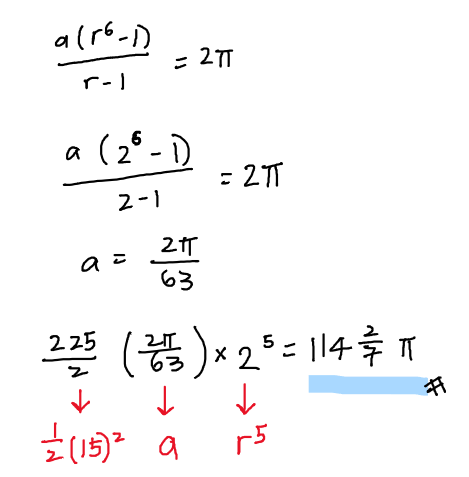
Hope this helps! 
Now I understand  Thank you very much !
Thank you very much ! 

I found some biology trials paper too 

https://drive.google.com/drive/folders/109mrYI2Nv6tF0tyZVOeCpNbQ8FiiQTIQ
You’re welcome Farhaini, and thank you for sharing the link 
It’s my pleasure