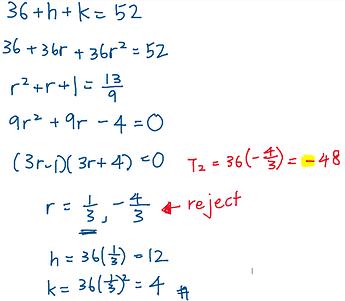Question
10 (a) Diberi tiga sebutan pertama untuk janjang aritmetik adalah 12-x, 18 dan 4x.
Cari nilai x.
Given the first three terms of an arithmetic progression are 12-x, 18 and 4x.
Find the value of x. [2 markah/ marks](b) Tiga sebutan positif berturutan bagi suatu janjang geometri ialah 36, h dan k. Diberi bahawa hasil tambah sebutan-sebutan itu ialah 52. Cari nilai bagi h dan k.
Three consecutive positive terms of a geometric progression are 36, h and k. It is given that the sum of the terms is 52. Find the value of h and k. [3 markah/ marks]
Answer
Hi Farhaini,
Good question, you can use both actually! Even for A levels they only gave the 1-r formula to avoid confusion, since you will actually get the same answer no matter which formula you use.
Only for the sum to infinity case, you have to use the 1-r formula and |r| must be less than 1, but for this question, this is not the case.
We reject r=1 because in a GP r can never be 1, otherwise h and k will also be 36, and 36+36+36 is definitely not equal to 52.
We reject -\frac{4}{3} because the question says 3 consecutive positive terms. If you use r=-\frac{4}{3} and treat 36 as the first term (T_1), then your h (T_2) will be negative, which doesn’t meet the question’s requirement.
So we are only left with r=\frac{1}{3}, since r is positive, then all numbers in the GP will be positive. Then we substitute it to find h and k.
Second method
This is my method where I express the equation in terms of r only. I don’t get a cubic equation like the method you suggested but rather a quadratic equation, but I still get the same answer.
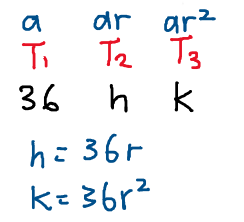
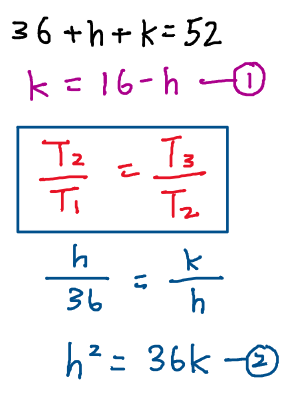
Mark scheme method
For the mark scheme they did not use r at all, they just solved it using simultaneous equation. So they don’t need to substitute r and they can get h directly.

Hope this helps! 
Wowww I never thought there are so many ways to solve this question 

 Thank you very much!
Thank you very much!