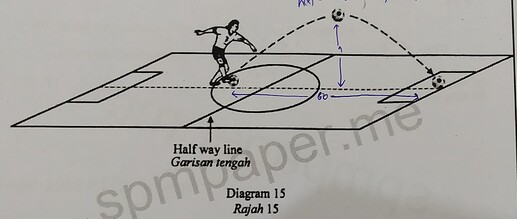
15 Diagram 15 shows a football player kicked a ball 5 \mathrm{~m} from the left of the half way line of football field.
Rajah 15 memenjuktan seorang pemain bola sepak menendang sebiji bola 5 \mathrm{~m} dari sebelah kiri garisan tengah padang bola.
The locus of the ball is represented by the function h(x)=-\frac{1}{100} x^{2}+4 p x-2 q+5. The ball reaches the maximum height of 9 \mathrm{~m} and touches the ground 60 \mathrm{~m} from where it was kicked.
Find the value of p and of q. [4 marks]Lokus bola itu diwakili oleh fungsi h(x)=-\frac{1}{100} x^{2}+4 p x-2 q+5 . Bola itu mencapai ketinggian maksimum 9 \mathrm{~m} dan menyentuh permukaan padang 60 \mathrm{~m} dari bola itu ditendang.
Cari nilai p dan nilai q. [4 markah]
1 Like
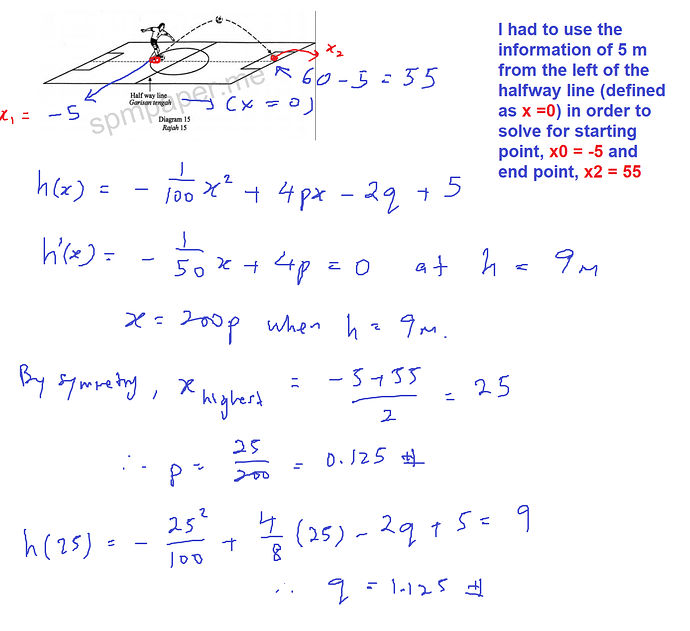
Hi Bernard, maybe you have a different approach, but I had to use 5 m from the left in order to solve for the missing start point (x = -5) and the end point of x = 55 in order to use the given locus equation.
My own solution (may be different from ans. scheme) attached as shown.
1 Like
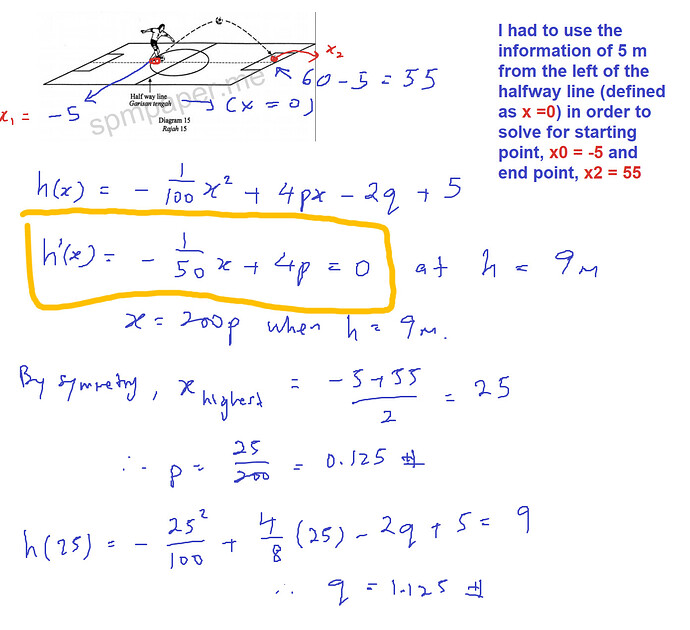
I did differentiation of the locus equation in order to find the maximum point, since dh/dx = 0 at the maximum point and it allows me to find out p easily.
1 Like
Ohhh I see. OK, Thanks!!
1 Like