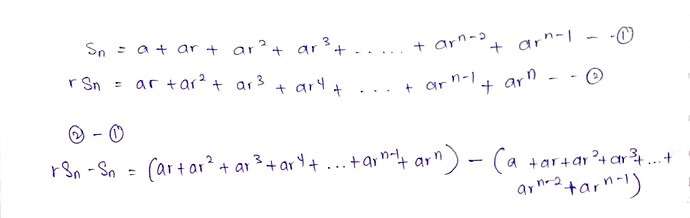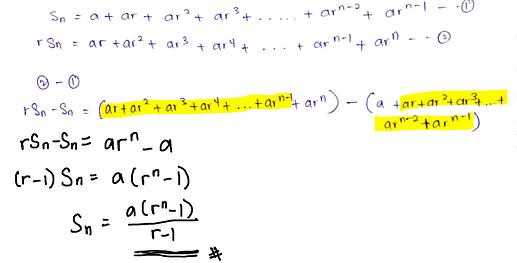Question
5(a) Diberi suatu janjang geometri dengan sebutan-sebutan a, a r, a r^{2}, a r^{3}, \ldots, a r^{n-2}, a r^{\prime \prime-1} dan hasil tambah n sebutan pertama ialah S_n.
Terbitkan rumus hasil tambah n sebutan pertama, S_{n} bagi janjang geometri apabila |r|>1.Given a geometric progression with terms a, a r, a r^{2}, a r^{3}, \ldots, a r^{n-2}, a r^{n-1} and the sum of first n terms is S_n.
Derive the formula for the sum of the first n terms, S_{n} for the geometric progression when |r|>1.
[3 markah]
[3 marks]
Answer
Hi Farhaini,
Your working is in the right direction actually, and you’re almost there!
You can see that in the picture below in the two parts where I highlighted in yellow, the terms are actually all the same and we can cancel them off.
Hope this helps! 
Ohhh I just realized that we can cancel it out Thank you very much !