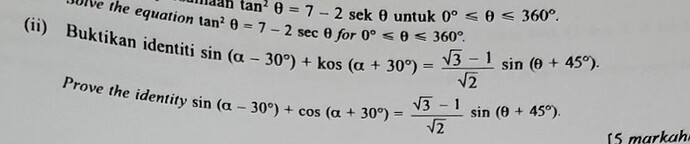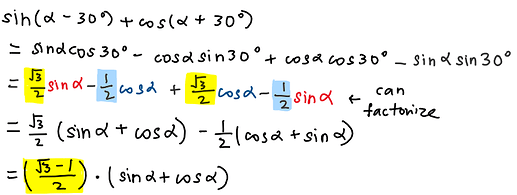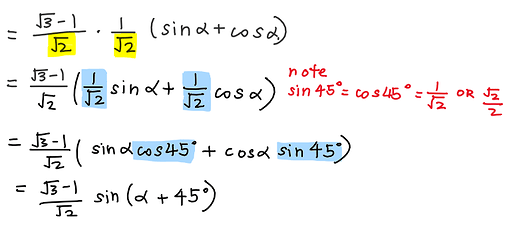Question
(ii) Buktikan identiti \sin \left(\alpha-30^{\circ}\right)+\operatorname{kos}\left(\alpha+30^{\circ}\right)=\frac{\sqrt{3}-1}{\sqrt{2}}\sin \left(\theta+45^{\circ}\right)
Prove the identity \sin \left(\alpha-30^{\circ}\right)+\cos \left(\alpha+30^{\circ}\right)=\frac{\sqrt{3}-1}{\sqrt{2}} \sin \left(\theta+45^{\circ}\right)
Solution
Hello Farhaini, your first step is correct. I think you got a bit lost after expanding using the double angle formula, notice that you can factorize after expanding.
And here’s the trick: split the 2 in the denominator to \sqrt{2} \times\sqrt{2} ! Why? Because at the RHS of the equation, the expression is sin(\theta + 45) , and the denominator is a \sqrt 2.
Also, I’m not sure why did the question use \theta instead of \alpha on the RHS, the unknown shouldn’t change though, could be typing error.
Hope this helps! 
Ohhh Thank you very much !