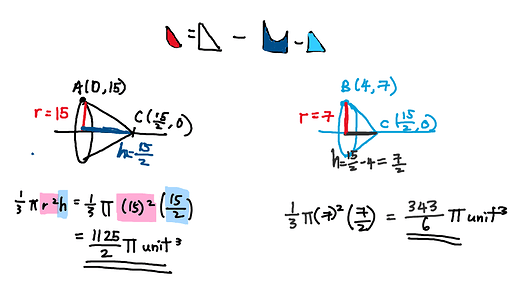Someone please help me 





Thank you so much
Question
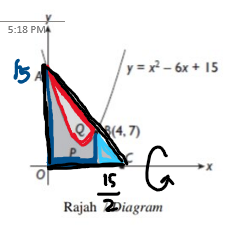
- Rajah menunjukkan garis lurus A C menyilang lengkung y=x^{2}-6 x+15 pada titik A dan titik B.
Diagram shows the straight line AC intersects the curve y=x^{2}-6 x+15 at point A and point B.
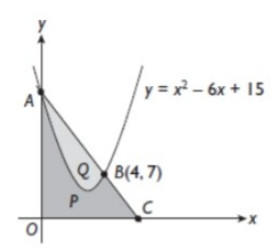
Rajah / Diagram
(a) Hitung luas rantau berlorek P.
Calculate the area of the shaded region P.
[5 markah/marks]
Jawapan / Answer: 45 \frac{7}{12} \mathrm{~cm}^{2}
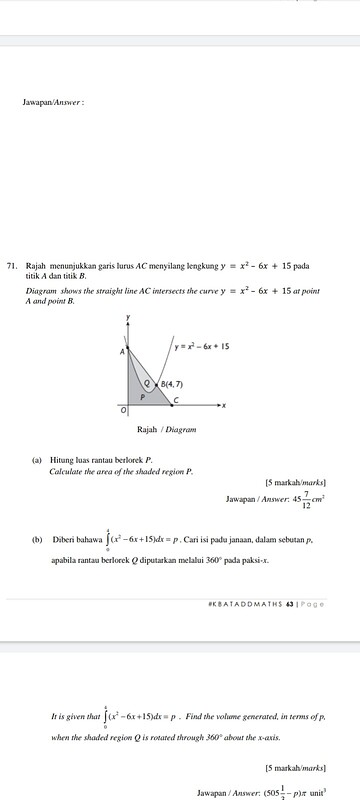
(b) Diberi bahawa \int_{0}^{4}\left(x^{2}-6 x+15\right) d x=p. Cari isi padu janaan, dalam sebutan p, apabila rantau berlorek Q diputarkan melalui 360^{\circ} pada paksi- x.
It is given that \int_{0}^{4}\left(x^{2}-6 x+15\right) d x=p. Find the volume generated, in terms of p. when the shaded region Q is rotated through 360^{\circ} about the x-axis.
[5 markah/marks]
Jawanan/Answer: \left(505 \frac{1}{3}-p\right) \pi unit^3
Solution
Hello! Whenever you come across integration questions, ask yourself: how do I break down the shapes into several parts in a way that is easy for me to solve?
This is how I split the shapes:
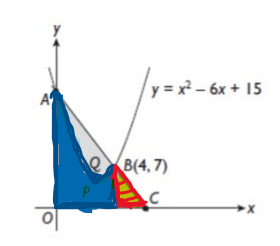
The triangle seems easy to solve right? We just need the coordinate of C.
For the area shaded in blue, it’s also fairly simple: integrate the curve with respect to x from 0 to 4.
But we don’t know the coordinate of C, so we’ll start with the blue area first.
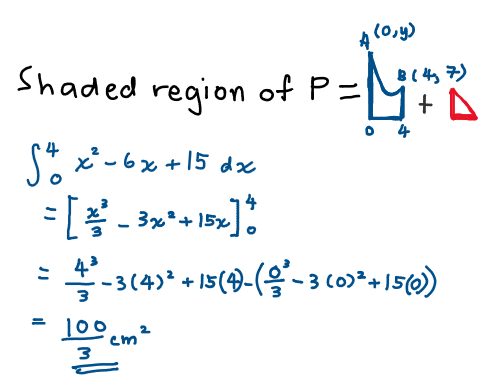
All we have left is the red triangle, but firstly, how to find the coordinate of C? Well, A, B and C lies on the same line and notice that at the beginning of the question, it is mentioned that: curve intersects at point A. So we can find the coordinate of A from there. A lies on the y-axis, so x-coordinate of A is 0, substitute x=0 into the equation of the curve and solve for the y-coordinate. (This value of y-coordinate is also the y-intercept of line ABC.) From there, we can then find coordinate C using the equation of a straight line concept.
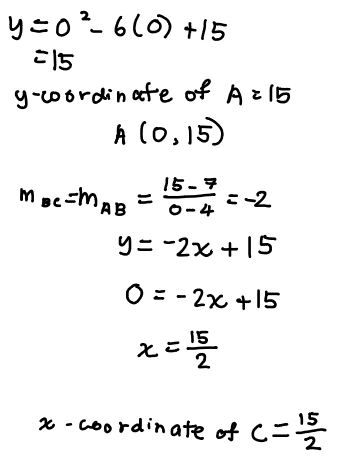
The last two steps are pretty simple: find the area of the triangle and add the two areas!
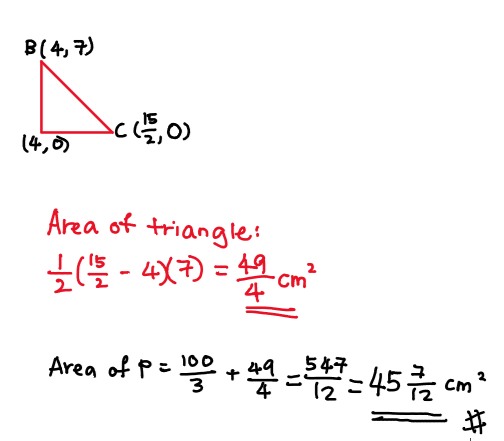
Hope this helps! Will upload the solution to part b in a while! 
Hello again Dhaksheina, sorry for the rather late reply,
I do think there is a high chance that the question is missing a square outside the bracket, but it is best if you could confirm it with your teacher!

Here is my solution to part b:
I personally prefer using the volume of a cone formula as it is quicker and harder to make errors, but you could also integrate the straight line to find the volume!

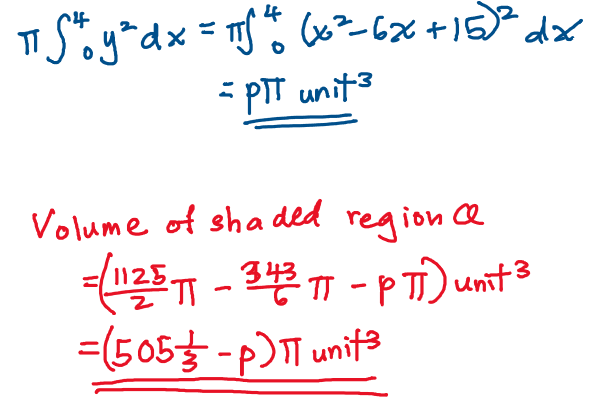
Hope this helps!