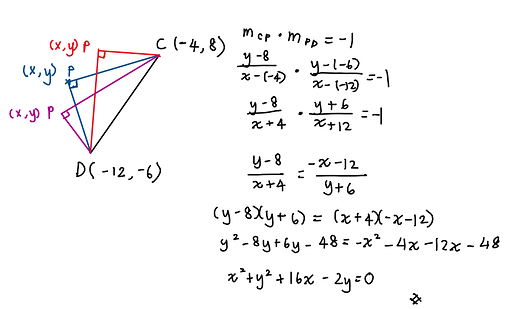Question
Subjektif Respons Terhad Berstruktur
Penyelesaian secara lukisan berskala tidak díterima.
Solution by scale drawing is not accepted.
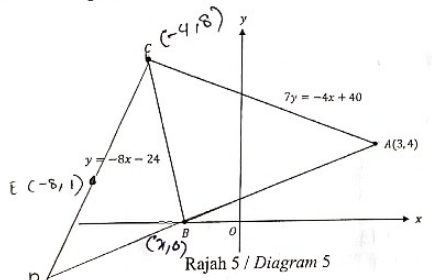
Rajah 5 menunjukkan segi tiga ABC.
Diagram 5 shows the triangle ABC.
(a) Hitungkan koordinat bagi titik C.
Calculate the coordinate of point C.
[2 markah / 2 marks](b) (i) Garis lurus AB dipanjangkan ke suatu titik D dengan keadaan A B:B D=2:3 . Cari koordinat D.
The straight line AB is extended to a point D such that A B:B D=2: 3 . Find the coordinate of D.
[2 markah / 2 marks](ii) Carikan luas bagi \triangle ACD, Seterusnya, hitungkan nisbah bagi luas segi tiga ABC kepada luas segi tiga ACD dengan keadaan luas \triangle ABC ialah 26 unit^2.
Find the area for \triangle ACD. Hence, calculate the ratio of triangle ABC to triangle ACD such that area of \triangle ABC is 26unit^2
[3 markah / 3 marks](c). Diberi titik E(-8, 1), ialah titik tengah bagi garis lurus CD. Titik P(x, y) bergerak dengan keadaan \angle CPD=90^{\circ}. Cari persamaan lokus P.
Given point E(-8,1) is midpoint of straight line CD. Point P(x, y) moves such that \angle CPD= 90^{\circ}. Find the equation of the locus P.
[3 markah/ 3 marks]
Answer
Hi Farhaini,
The keyword in question c is \angle CPD = 90^{\circ}. What do we know about two lines perpendicular to each other? Well, we can use the formula m_1m_2=-1.
Here is my working for your reference:
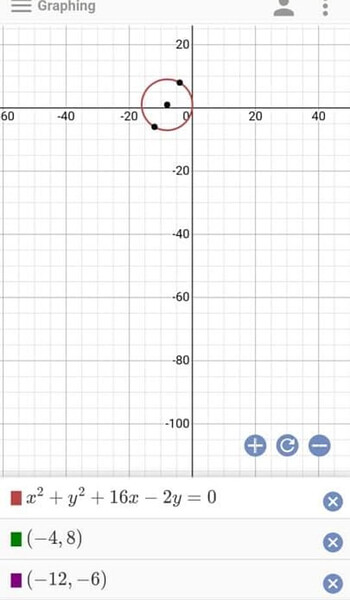
If you are having a hard time visualizing the shape of the locus, this is how it looks like:
Further clarification:
Actually, the locus is a circle with centre E, but it is best not to use the equation of a circle to solve this question in my opinion, even though you will end up with the same final answer. The reason is that even though the locus is a circle, P cannot be at C and D, if not the
\angle CPD = 90^{\circ} condition will not be fulfilled. (as CPD will be a straight line). You also notice that if P is at C and D, then the equation m_{CP}m_{PD}=-1 will not be satisfied because for either gradient you will get \frac{0}{0} which is undefined. And you cannot get that exclusion from using the equation of a circle.
Hope this helps! 
Ohh I see Thank you very muchh!