SPM AddMaths Questions
10 (a) There are 4 girls and 3 boys to be arranged in a row for a photograph session. Find the number of ways to arrange them if the 3 boys want to sit side by side.
Terdapat 4 orang murid perempuan dan 3 orang murid lelaki hendak disusun dalam sebaris untuk satu sesi fotografi. Cari bilangan cara untuk menyusun mereka jika 3 orang murid lelaki itu mahu duduk bersebelahan. [3 marks/3 markah]
SPM AddMaths Solution
Keywords: 3 boys want to sit side by side
Therefore, the girls can sit together or they can sit separately.
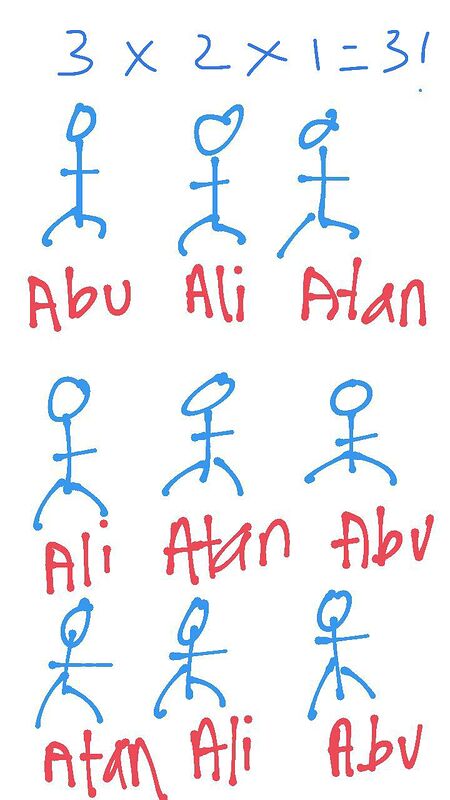
Let’s visualize this diagram
•The first person/group can be chosen from one of the groups
There are 5 groups that can be chosen for the first box. For the second box, there are only 4 groups left so there are only 4 groups of people that can be chosen and followed by 3…2…1.
Therefore, 5×4×3×2×1= 5!
Next, don’t forget that the boys in the group can also sit in different ways.
Let’s visualize this diagram too.
Thus, 3×2×1=3!
The last step is we must multiply both of the number of ways :
5! × 3! = 720
ANSWER: 720 ways
SPM AddMaths Question
(b) A teacher committee that consists of 5 teachers is to be chosen from 4 male teachers and 4 female teachers. Find the number of different ways the committee can be formed if at least one male teacher must be selected.
Suaru jawatankuasa guru yang terdiri daripada 5 orang guru akan dipilih daripada 4 orang guru lelaki dan 4 orang guru perempuan. Cari bilangan cara berlainan jawatankuasa itu boleh dibentuk jika sekurang-kurangnya seorang guru lelaki mesti dipilih. [3 marks/3 markah]
SPM AddMaths Solution
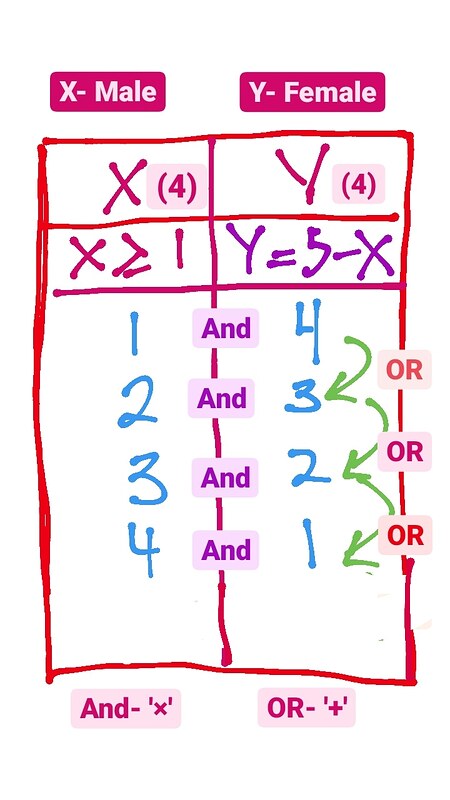
I always solve this question by using box…you can use this method too🥳
First we must know that the arrangement for this question is not important. Thus, we must use this formula : nCr
The question state that at least one male teacher must be selected. So maybe 1 male tcr is selected OR 2 male teacher selected OR 3 OR 4 so we must ’ + ’ . If 2 male tcr selected.Of course 3 female tcr will be selected bcz the total must be 5 . 2 male tcr and 3 female tcr / 4 male tcr and 1 female tcr so we must ‘×’
Therefore, (4C1 × 4C4) + (4C2 × 4C3) + (4C3 × 4C2) + (4C4 × 4C1) = 56 ways
Note : if the word AND we must ’ × ’ and if the word OR we must use ’ + ’
I hope you can understand.
ANSWER: 56 WAYS
I made a mistake. I am sorry ya but don’t worry I already corrected it😊