Hi, may I know how to solve this question? And do you have any advice for this chapter? This chapter really drives me crazy🤯 Thank you!
Question
12.5 \mathrm{~g} of crystals of copper(II) sulphate, \mathrm{CuSO}_{4} \cdot 5 \mathrm{H}_{2} \mathrm{O} are stirred into distilled water to make solution of concentration 1.5 \mathrm{~mol} \mathrm{dm}^{-3}. What is the volume of the solution obtained?
[Relative atomic mass: \mathrm{H}=1; \mathrm{Cu}=64, \mathrm{~S}=32, \mathrm{O}=16 ]
A 15.0 \mathrm{~cm}^{3}
B 33.3 \mathrm{~cm}^{3}
C 100 \mathrm{~cm}^{3}
D 150 \mathrm{~cm}^{3}
Answer
Hi Jane,
I believe that your answer is correct.
The n \space\mathrm{=\frac{MV}{1000}} (where n = number of moles)
is one of the key formulas in the chapter, and I think for most questions it is important to find out the number of moles first, if the given information allows it.
Here, we are not given V, but we can still find the number of moles of \mathrm{CuSO_4} used because the question gives us information regarding relative atomic mass. By adding the given relative atomic masses to find the relative formula mass, we can then find the number of moles.
number of moles can be found by using: mass used \div relative formula mass
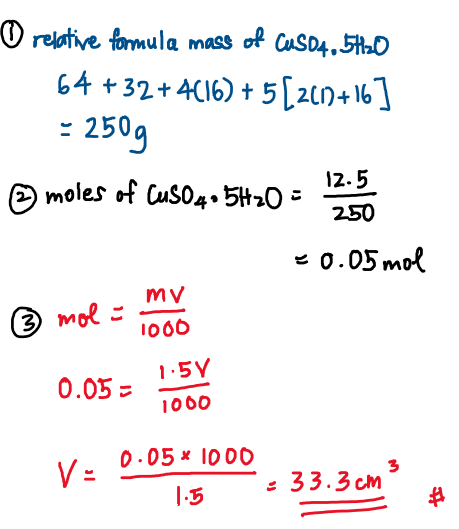
For making stock solution (whether by dissolving solid or by diluting liquid), the number of moles of the solid being dissolved / liquid being diluted doesn’t change. (because we are not pouring away the solid or liquid, only adding more distilled water to it)
Only the concentration changes: concentration decreases as you add more volume, obeying the logic of the formula n \space\mathrm{=\frac{MV}{1000}}.
Maybe more topical practices of reference book exercises / state modules / state trial papers will help, and really try to understand what is actually happening and why the formula works. Hope this helps! 
Okie! Thank you so much☺️
