Soalan
13 (a) Diberi persamaan linear y=2 x-5 Tanpa melukis graf garis lurus, tentukan sama ada titik-titik yang diberikan memuaskan y=2 x-5, y<2 x-5 atau y>2 x-5.
Given a linear equation y=2 x-5. Without drawing a straight line graph, determine whether the given points are satisfies y=2 x-5, y<2 x-5 atau y>2 x-5. [6 markah/marks]
(i) (1,-4)
(ii) (3,1)
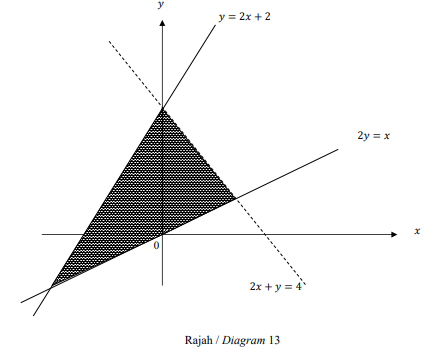
(iii) (-2,2)(b) Tulis tiga sistem ketaksamaan linear yang memuaskan rantau berlorek dalam Rajah 13 di bawah.
write three linear inequalities system that defines the shaded region in Diagram 13 below. [3 markah/marks]
Jawapan
Hai Farag,
Untuk soalan (a) , kita gantikan nilai koordinat-x dalam ungkapan 2x-5, dan bandingkan nilai yang dikira dengan nilai koordinat-y.
Bahagian (i):
nilai koordinat-y adalah kurang daripada nilai 2x-5 yang dikira.
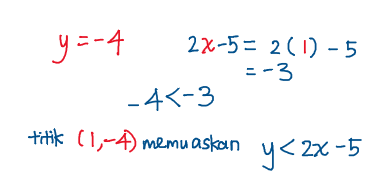
Bahagian (ii):
nilai koordinat-y adalah sama dengan nilai 2x-5 yang dikira.
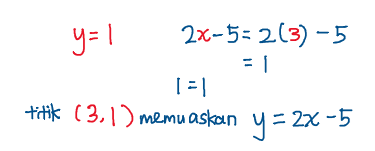
Bahagian (iii):
nilai koordinat-y adalah lebih daripada nilai 2x-5 yang dikira.
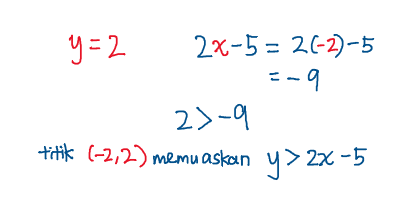
Untuk soalan (b) pula,
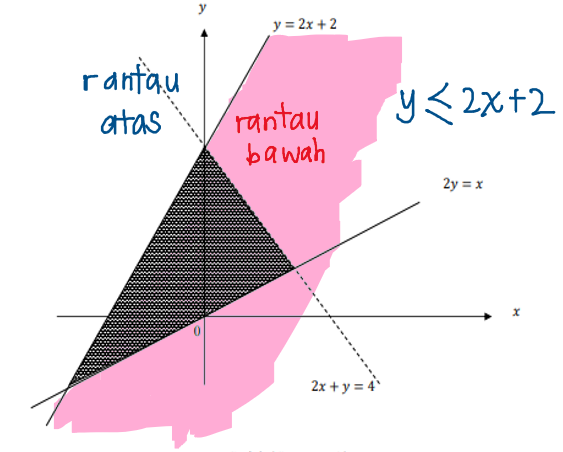
Rantau berlorek berada di bawah garisan y=2x+2, dan garisan y=2x+2 dalam graf adalah lurus, jadi ketaksamaan linear yang pertama ialah y \leq 2x + 2
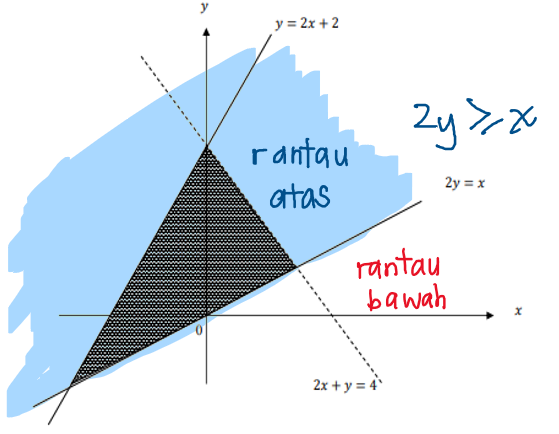
Rantau berlorek berada di atas garisan 2y=x, dan garisan 2y=x dalam graf adalah lurus, jadi ketaksamaan linear yang kedua ialah 2y \geq x
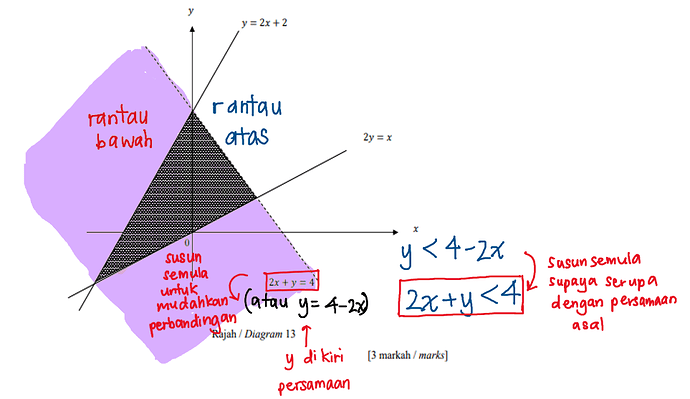
Rantau berlorek berada di atas garisan 2x+y=4, dan garisan 2x+y=4 dalam graf adalah putus-putus, jadi ketaksamaan linear yang ketiga ialah 2x + y < 4
Ingat: y haruslah sentiasa berada di kiri persamaan ketika hendak menbuat
perbandingan.
Maklumat ekstra:
Berhati-hati ya, jika persamaan itu ialah 2x-y=4 dan bukan 2x+y=4, kita sepatutnya susun semula persamaan supaya jadi y=2x-4, dan baru bandingkan persamaan yang disusun dengan rantau berlorek. Harap gambar di bawah memberikan penerangan yang lebih jelas:
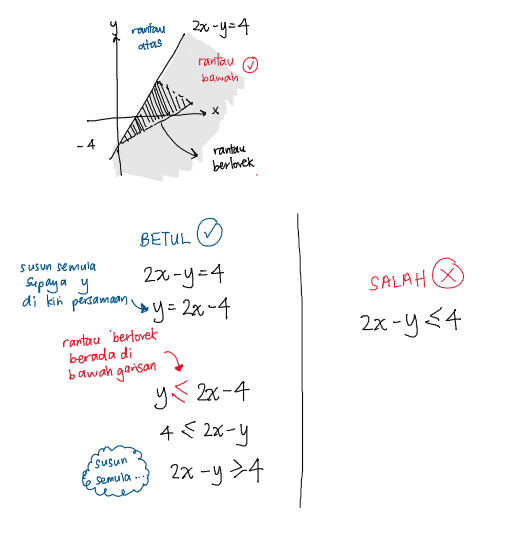
Harap Farag dapat muat naik jalan kerja untuk pertanyaan yang lain pada masa akan datang supaya dapat bantu Farag mengesan kesilapan atau mendorong Farag dengan lebih efektif 
Terima Kasih kerana telah membantu saya