[SPM Maths Quadratic Functions and Equations] How to do a) (ii) and (iii)?

[Anonymous_want_12A]

Answers:
(i) p=2
(ii) q=6
(iii) a=-1

[Far]

Maths Quadratic Functions and Equations Question

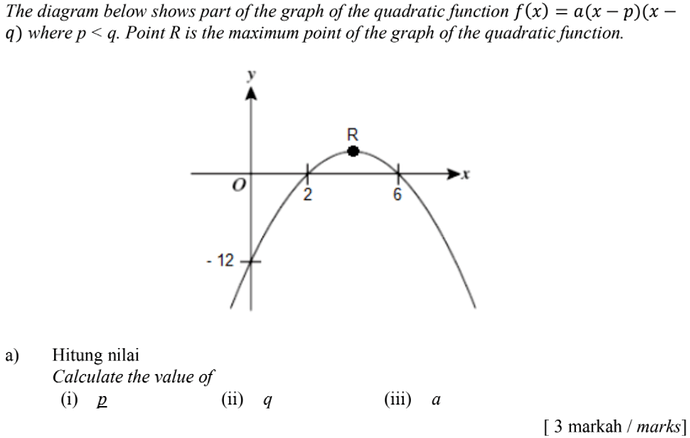
The diagram below shows part of the graph of the quadratic function f(x)=a(x-p)(x-q) where p<q. Point R is the maximum point of the graph of the quadratic function.

a) Hitung nilai Calculate the value of
(i) \underline{p}
(ii) q
(iii) a
[3 markah / marks]

Maths Quadratic Functions and Equations Solution

Hello!

Quadratic equation can be written in three different forms: standard, factored and vertex.

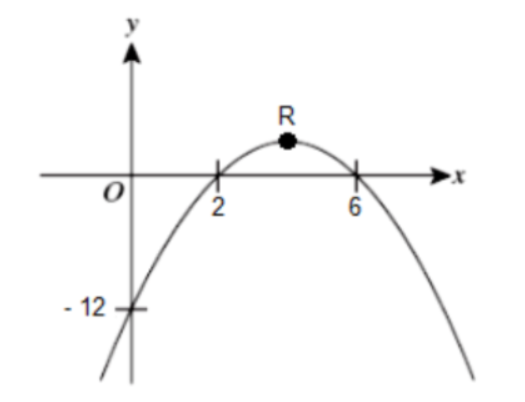
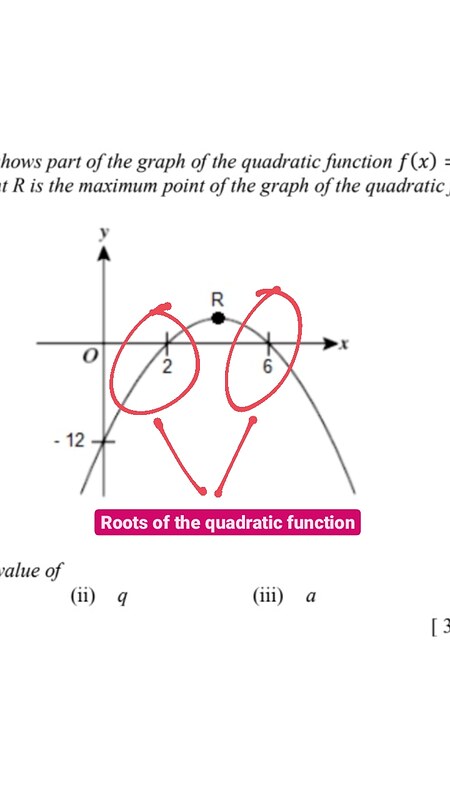
f(x)=a(x-p)(x-q) is the factored form, where p and q represent the roots of the equation.

The roots of a quadratic equation are the x-intercepts of the graph.

So we know that p and q are the roots of the equation where p is smaller than q (p<q )

Thus, p = 2 and q= 6

To find the value of a we can substitute the values of p and q into the equation and also the coordinate of y- intercept, which is (0, -12)

Where, x=0 and f(x) = -12

f(x)=a(x-p)(x-q)

-12=a(x-2)(x-6)

-12=a(0-2)(0-6)

-12=a(-2)(-6)

-12=a(12)

a=(-12)/(12)

a= -1

ANSWERS: p=2,q=6,a=-1

[Anonymous_want_12A]

Ohhhh I see, thank you so much!!

[Far]

You are welcome