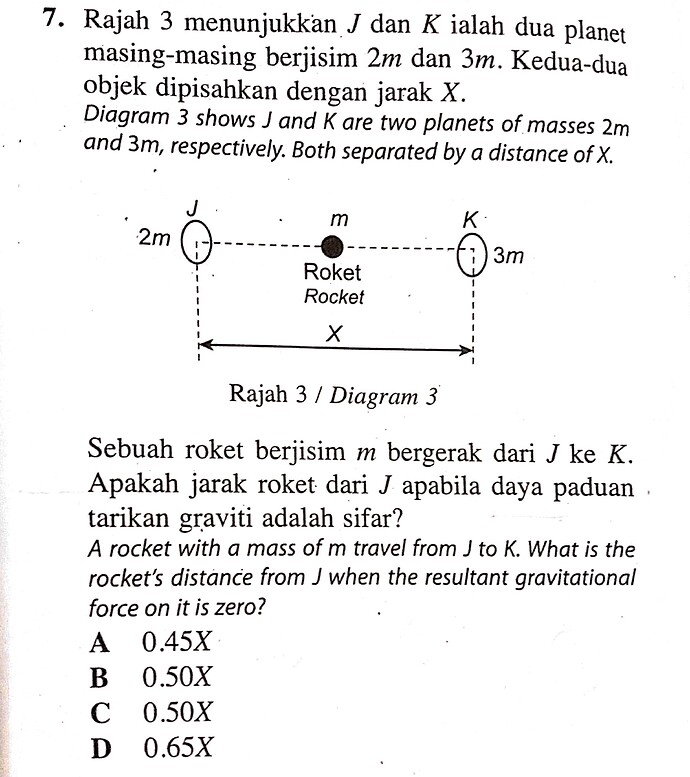
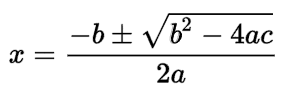- Rajah 3 menunjukkan J dan K ialah dua planet masing-masing berjisim 2 m dan 3 m. Kedua-dua objek dipisahkan dengan jarak X.
Diagram 3 shows J and K are two planets of masses 2 \mathrm{~m} and 3 \mathrm{~m}, respectively. Both separated by a distance of X.

Rajah 3 / Diagram 3
Sebuah roket berjisim m bergerak dari J ke K. Apakah jarak roket dari J apabila daya paduan . tarikan graviti adalah sifar?
A rocket with a mass of m travel from J to K. What is the rocket’s distance from J when the resultant gravitational force on it is zero?
A \quad 0.45 X
B \quad 0.50 X
C \quad 0.55 X
D \quad 0.65 X
We solve this using Newton’s Law of Gravitation:
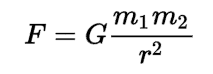
Assuming the rocket is located in a linear line between J and K, there will be TWO forces, acting on the rocket in opposite directions. Let force by J on the rocket be Fⱼ, force by K on rocket be Fₖ.
Let distance between J and rocket be x, and distance between rocket and K be X-x.
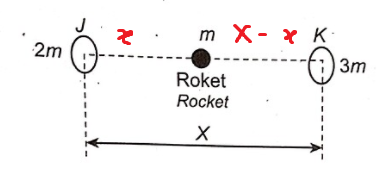
Calculate force by J on rocket:
Fⱼ = G(2m)(m)/x² = 2Gm²/x²
Calculate force by K on rocket (opposite direction):
Fₖ = -G(3m)(m)/(X-x)² = -3Gm²/(X-x)²
When the resultant gravitational force on it is zero, this implies the magnitude of Fⱼ = Fₖ.
2Gm²/x² = 3Gm²/(X-x)²
Solving the quadratic equation,
2(X² - 2Xx + x²) = 3x²
Remember, take X as a “known” value, and x as the unknown, rearranging in terms of quadratic equation with respect to “x”,
x² + 4Xx - 2X² = 0
Using the quadratic formula,
Where a = 1, b = 4X, a = 1 , c = -2X²
x = [-4X ± sqrt(16X² - 4(1)(-2X²))]/2
Taking only the positive root since distance between J and rocket must be positive (x > 0),
x = [-4X + sqrt(24X^2)]/ 2 = [-4X + 2sqrt(6) X]/2 = (sqrt(6) - 2) X = 0.45 X
Therefore, answer is A. 0.45 X
I must say, this is an interesting application of ADD MATHS in Physics.
Wahh it’s really an interesting explanation. Thank you very much